約数の個数の公式と平方数の性質
約数の個数は「素因数分解して」「それぞれの指数(右上の小さい数字)に1を足して」「全部かける」ことで計算できる。

約数の個数の公式について,計算例・証明・おもしろい応用例を整理しました。
約数の個数の公式の使用例
約数の個数の公式の使用例
の約数の個数はいくつか?
約数の個数は「素因数分解して」「それぞれの指数に1を足して」「全部かける」ことで計算できます。200の約数の個数は,
- 「素因数分解」:
- 「指数に1を足す」:
- の指数は なので1を足すと 4
- の指数は なので1を足すと 3
- 「全部かける」:,つまり約数の個数は 個
ちなみに, の約数を列挙すると で確かに 個あります。
練習問題
大きい数の約数の個数を計算したい場合,1つずつ約数を数えるのは大変ですが,公式を使えば素早く計算できます。
の約数の個数は?
素因数分解されているので,約数の個数は「それぞれの指数に1を足して」「全部かけあわせる」と
とてつもなく大きい数なので,約数を全部列挙して数えるのは無理です!
約数の個数の公式の証明
約数の個数の公式の証明
約数の個数が,なぜ「素因数分解して」「それぞれの指数に1を足して」「全部かけあわせる」ことで計算できるのか解説します。

例えば を素因数分解すると です。 の指数を の中から一つ, の指数を の中から一つ選ぶと約数が決まります。
よって約数の個数は 個です。
一般の場合も同様です。
の約数について考える。素因数分解された形を とする。 の約数は (ただし,各 に対して は を満たす整数, は素数)という形の整数だけであり,これで全ての約数を表せる。
そのような の選び方は 通りである。
つまり,約数の個数は「素因数分解して」「それぞれの指数に1を足して」「全部かけあわせる」と計算できる。
平方数の約数の個数は奇数
平方数の約数の個数は奇数
約数の個数の公式から導ける重要な定理を紹介します。
正の整数 について,
が平方数 の約数の個数は奇数
-
は平方数である。約数は の5個(奇数個)
-
は平方数でない。約数は の6個(偶数個)
と素因数分解されているとき, が平方数であるというのは,平方数の定義より がいずれも偶数であることと同値。
一方, の約数の個数が奇数であるというのは,約数の個数の公式より が奇数であることと同値。
これは がいずれも偶数であることと同値。
このように約数の個数の公式を使えば鮮やかに証明できますが,この公式を使わずとも以下のように証明できます。
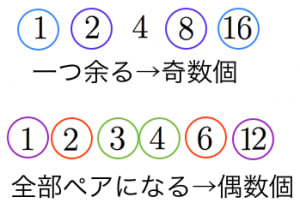
が の約数のとき, も の約数である。このことに注意すると, の約数を小さい順に と並べたとき, などが成立する。つまり,大きい方と小さい方から一つずつとってくるとかけて になるペアができる。
が平方数のときは となる約数 が存在するので真ん中で一つ余る。それ以外は全てペアになる。よって約数の個数は奇数。
が平方数でないときは となる正の整数 が存在しないので,全てペアになる。よって約数の個数は偶数。
最短で得点力を上げる!高校数学の問題集〈典型250問〉の問題128では,この性質を使う問題と2通りの解法を紹介しています。
なお,この考え方を使う問題が国際数学オリンピックで出題されたこともあります。
単に「約数」と言うと「負の数」を含むかどうかがあいまいですね(この記事をはじめ,当サイトでは「正の約数」のことを単に「約数」と書いている箇所があります,ご注意ください)。











