エラトステネスのふるいとその計算量
更新
エラトステネスの篩(ふるい)とは, 以下の素数を全て見つけ出す高速な方法です。
エラトステネスのふるいの概要と,愚直に計算するよりも速いこと(計算量が であること)を紹介します。
愚直な方法
愚直な方法
エラトステネスのふるいの前に,まずは愚直な方法で 以下の素数を全て列挙することを考えてみます。
-
から まで順々に素数かどうか判定する。
-
が素数かどうかは 以下の素数たちで割り算すればよい。
が登場したのは が合成数なら必ず より小さい素因数を持つからです。
例えば が素数かどうか判定するときに なので 以下の素数で割り切れないことを証明すればOKです。つまり「 の倍数でない, の倍数でない, の倍数でない」ことを確認すればOKです。
エラトステネスのふるい
エラトステネスのふるい
-
から までの整数を並べる。
-
生き残っている数の中で一番小さい(かつまだ として使われていない)ものを新たに とおき, 以外の の倍数を全て消していく。
-
2の操作を繰り返していき, が を越えたら終了。最終的に生き残ったものが素数。
で実験してみます。
-
から までの整数を並べる。
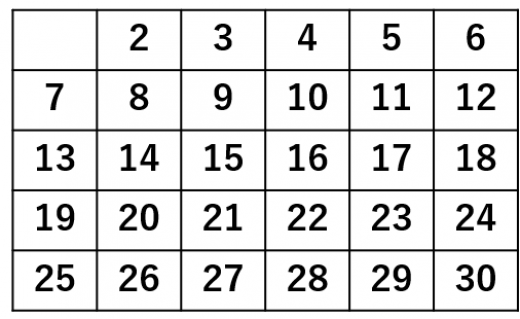
-
の倍数をふるい落とす

-
の倍数をふるい落とす

-
の倍数をふるい落とす
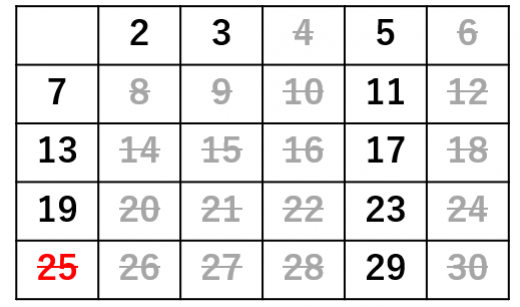
-
次は となるが より大きいので終了。 以下の素数は,ここまで生き残った である!
合成数は として選ばれる前にふるい落とされるので, として選ばれるのは素数のみです。つまり「 以下の素数」回だけ上記のふるい落とす操作を行うことになります。
エラトステネスのふるいの計算量
エラトステネスのふるいの計算量
エラトステネスのふるいによる計算量を考えてみます。ただし,ここで言う計算量とは が大きいとき,アルゴリズムの遂行に必要な基本演算(四則演算など)の回数を大雑把に評価したものです。定数倍くらいの違いなどは無視して)大雑把に であるような量を と書きます。→オーダー記法(ランダウの記号)の定義と大雑把な意味
以下のように実装した場合を考える。
- 要素数 ですべての要素が である配列 を用意しておく
- のすべての の倍数番目の要素に を代入する
- のすべての の倍数番目の要素に を代入する
- のすべての の倍数番目の要素に を代入する
- 以下の素数まで続ける
- 最後に の各要素を見て であるのが何番目かを列挙する
手順1と手順6の計算量は である。残りの手順については, でふるいおとすのに 回, でふるい落とすのに 回, でふるい落とすのに 回, の定数時間の演算(配列への代入)を行うので計算量は,
(ただし,和は 以下の素数全体に関して取る)
ここで が十分大きいとき までの素数の逆数和はだいたい くらい(→素数の逆数和が発散することの証明)なので,計算量は となる。
愚直な方法による計算量との比較
愚直な方法による計算量との比較
最初に紹介した愚直な方法による計算量も求めてみます。
が素数かどうかを判定するのに最大 回くらいの割り算が必要なので,全体の計算量はおおよそ
これは が大きいとだいたい
よって,計算量は
と とでは が大きいとき圧倒的に前者の方が計算量が少なくなります(対数関数でさえ増加が遅いのだから はもっと遅い!)。エラトステネスのふるいの素晴らしさがなんとなく分かっていただけたかと思います。
なお,素数定理とかを使えば愚直な方法に対してもう少し計算量を厳しく評価できますが,それでもエラトステネスのふるいの方が速いです。
素数の逆数和が出てくるのは楽しいですね。











