原始ピタゴラス数の木
更新
すべての原始ピタゴラス数は, に対して,3つの行列 のどれかをかける操作を何度か繰り返すことで作れる。ただし,
,
,
ピタゴラス数に関する非常におもしろい定理です。この定理の主張と証明を詳しく解説します。
定理の主張について
定理の主張について
を満たす正の整数の組 のことをピタゴラス数と言います。その中で, の最大公約数が であるものを原始ピタゴラス数と言います。→ピタゴラス数の求め方とその証明
例えば, なので, は原始ピタゴラス数ですが,実は,すべての原始ピタゴラス数が から(3種類の行列をかけることで)作り出せるというのが冒頭の定理です。
例えば, という原始ピタゴラス数は,
のように から作り出せます。
他にも, という原始ピタゴラス数は,
のように から作り出せます。
原始ピタゴラス数の木
原始ピタゴラス数の木
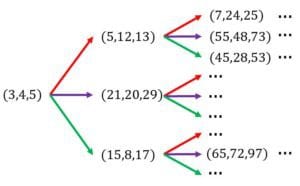
からはじめて,図のような木を書いてみます。赤い矢印が ,紫の矢印が ,緑の矢印が に対応します。
冒頭の定理は,上記の木に対して,
主張1.すべての原始ピタゴラス数が現れる
ですが,実は以下の主張も成立します。
主張2.原始ピタゴラス数以外のものは現れない
主張3.同じ原始ピタゴラス数が2度現れることはない
つまり,木をどんどん長くしていけば「余分なもの無しですべての原始ピタゴラス数をちょうど1回ずつ生成できる」というわけです。
※このページでは,原始ピタゴラス数と言ったときに第一成分が奇数で,第二成分が偶数であるもののみ考えます。例えば, は図に現れませんが, が現れます。
以下では,主張1~主張3を証明します。
主張2の証明
主張2の証明
まずは「原始ピタゴラス数以外のものは現れない」ことを証明します。
原始ピタゴラス数 に対して, , , も原始ピタゴラス数になることを示せばよい。
まず,
とおくと, となることが簡単な計算でわかる。
また, に注意すると, であることもわかる。よって, はピタゴラス数である。
次に, が原始ピタゴラス数でないと仮定する。つまり, がいずれも の倍数であると仮定する。すると, であり各成分が整数なので,
の各成分も の倍数になり, が原始ピタゴラス数であることに矛盾。よって, は原始ピタゴラス数である。
, についても同様である。ちなみに,
,
となる。
なお, をかける操作(およびその逆変換)において「第一成分が奇数で,第二成分が偶数」という性質が保たれることもわかります。
主張1と主張3の証明
主張1と主張3の証明
数学的帰納法を使って「すべての原始ピタゴラス数が,ちょうど1通りの方法で生成できる」ことを証明します。
まず, が最小の場合,つまり の場合について確認する。
の場合の原始ピタゴラス数は のみである。
また,原始ピタゴラス数に のいずれかをかけると第三成分は大きくなるので, が2回以上現れることはない。
次に「 であるすべての原始ピタゴラス数 が,ちょうど1通りの方法で生成できる」が正しいと仮定して, の場合でも正しいことを証明する。つまり, という原始ピタゴラス数があれば,それがちょうど1通りの方法で生成できることを証明する。
さて, , , という3つのベクトルを考えると,各成分が正であるものが1つだけ存在する(→※補足)
それが, であるとする(他の場合も同様)。
このとき, , はいずれかの成分が 以下なので,主張2により から生成することはできない。よって, の生成方法と, の生成方法は1対1に対応する。
また,このとき主張2の証明と同様にして, が原始ピタゴラスであることがわかる。さらに,三角不等式より第三成分は より小さいこともわかる。よって,帰納法の仮定により, は, からちょうど1通りの方法で生成できる。
よって, も からちょうど1通りの方法で生成できる。
※補足
※補足
最後に, , , という3つのベクトルを考えると,各成分が正であるものが1つだけ存在することを証明します。
が原始ピタゴラス数であるとき,ある正の整数 を用いて,
と表すことができます。→ピタゴラス数の求め方とその証明
よって,各成分を を用いて表すと,
よって, , , のいずれかが成立することに注意すると,各成分が正であるものが1つだけ存在することがわかる。
( である原始ピタゴラス数は だけであり, の場合は原始ピタゴラス数にならない)
余談
余談
各成分が整数で,行列式が または である行列を単模行列(たんもぎょうれつ,ユニモジュラ行列)と言います。 は単模行列のおもしろい例です!
参考文献:Trees of Primitive Pythagorean Triples(全43ページのPDF)
「もれなく重複なく」出てくるのがおもしろいです。ちなみに「もれなく重複なく」をかっこつけて「MECE(ミーシー)」と言うのはあまり好きではありません。











