複素数，虚数，純虚数，実数

更新日時 2023/07/26

複素数，虚数，純虚数の意味および関連する話題についてわかりやすく説明します。

複素数，虚数，純虚数の意味

複素数 とは，a+bia+bia+bi
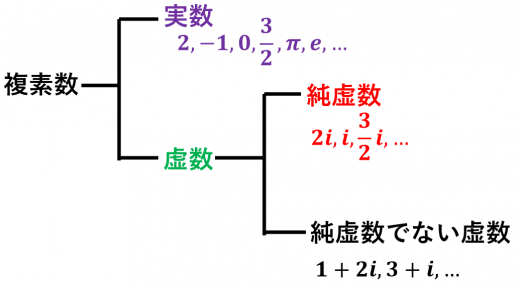
（a,ba,ba,b
は実数）という数全体のことです。iii は虚数単位と呼ばれ，
i2=−1i^2=-1i2=−1 を満たす数です。
複素数の中には実数と虚数があります。
虚数とは，a+bia+bia+bi
（a,ba,ba,b
は実数，b≠0b\neq 0b=0）という数全体のことです。
純虚数とは，虚数の中でも実部が 000，つまり a=0a=0a=0 である数のことです。ただし，000 は純虚数に含めません。

（純虚数に 000 を含めて考える場合もあります）
意味の違いをきちんと理解しましょう。

複素数平面上での複素数・虚数・純虚数

複素数平面上では，複素数・虚数・純虚数・実数は下図のように表せます。
複素数：平面全体
虚数：紫の横線以外全部
純虚数：赤い縦線
実数：紫の横線

複素共役と実数，純虚数

以下 $a, b$ は実数とします。複素数 $z=a+bi$ に対してその共役複素数を $\overline{z}=a-bi$ で定めます。→共役複素数の覚えておくべき性質

実数条件・純虚数条件

複素数 $z$ について，

$z$ が実数 $\iff z=\overline{z}$
$z$ が純虚数 $\iff z=-\overline{z}$ かつ $z\neq 0$

特に1つめはよく使います。

証明

$z=a+bi$ が実数
$\iff b=0$
$\iff a+bi=a-bi$
$\iff z=\overline{z}$

$z=a+bi$ が純虚数
$\iff a=0$ かつ $b\neq 0$
$\iff a+bi=-a+bi$ かつ $b\neq 0$
$\iff z=-\overline{z}$ かつ $b\neq 0$

複素数平面と実数，純虚数

平行条件・垂直条件
複素数平面上の相異なる4点
A(α)A(\alpha)A(α)，B(β)B(\beta)B(β)，C(γ)C(\gamma)C(γ)，D(δ)D(\delta)D(δ)
 について，
ABABAB
と
CDCDCD
が平行

  ⟺  α−βγ−δ\iff \dfrac{\alpha-\beta}{\gamma-\delta}⟺γ−δα−β​
が実数
ABABAB
と
CDCDCD
が垂直

  ⟺  α−βγ−δ\iff \dfrac{\alpha-\beta}{\gamma-\delta}⟺γ−δα−β​
が純虚数
複素数平面の基本的な公式集でも紹介した公式です。
平行
  ⟺  \iff⟺
偏角の差が
0∘0^{\circ}0∘
（または
180∘180^{\circ}180∘
）
垂直
  ⟺  \iff⟺
偏角の差が
90∘90^{\circ}90∘
（または
270∘270^{\circ}270∘
）
であることから分かります。
複素数の図形的な性質については，
1のn乗根の性質と複素数平面
複素数平面における直線の方程式
などでも解説しています。興味のある方はぜひご覧ください。
極形式複素数には，a+bia+bia+bi という表し方の他にも，reiθ=r(cos⁡θ+isin⁡θ)re^{i \theta}= r(\cos{\theta} + i\sin{\theta})reiθ=r(cosθ+isinθ) という表し方もあります。この表し方を極形式と呼びます。詳しくは 複素数平面における回転と極形式 をご覧ください。
なぜ複素数平面を考えるのか？複素数平面は xyxyxy 座標平面と似ていますが，
ベクトルの足し算を複素数の足し算で計算できる。
回転や拡大を複素数の掛け算で簡単に計算できる。
などの特徴があります。そのため，回転などを扱う場合は xyxyxy 座標で考えるよりも計算が楽になる場合が多いです。
虚数という言葉よりも複素数という言葉を使う機会の方が圧倒的に多い気がします。
Tag:数学２の教科書に載っている公式の解説一覧