複素数の範囲では累乗根は一般に複数個存在します。
1 の n 乗根
まずは 1 の n 乗根から調べていきましょう。
1 の2乗根は ±1 の2つでした。
1 の3乗根は 1 自身の他に ω=2−1+3i,ω2=2−1−3i があります。
一般に次の事実が成立します。
定理
n は正の整数とする。
1 の n 乗根は,複素数の範囲でちょうど n 個存在し,
en2kπi=cosn2kπ+isinn2kπ(k=0,1,⋯,n−1)
で過不足なく表される。
複素平面上に図示すると次のようになります。
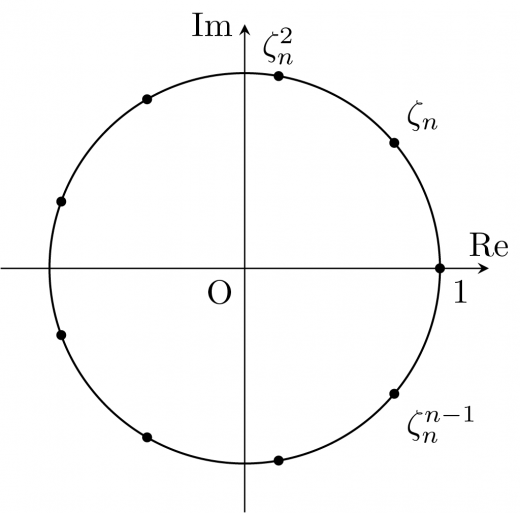
オイラーの公式 により en2kπi=cosn2kπ+isinn2kπ であることに注意しましょう。三角関数で表されることは「補足」の証明で用います。
証明
1 の n 乗根は,xn=1 の解である。
ゆえに xn=1 の解が,en2kπi(k=0,1,⋯,n−1) で過不足なく表されることを示せばよい。
- en2kπi はそれぞれ相異なる xn=1 の解であること
解であることは
(en2kπi)n=e2kπi=1 より従う。
相異なることを示す。
0≦p<q≦n−1 のとき en2pπi=en2qπi と仮定する。
-
辺々を en2pπi で割ることで
en2(q−p)πi=1
である。
-
0<q−p<n であることから en2(p−q)πi=1 である。(→補足を参照)
これらは矛盾する。
よって 0≦p<q≦n−1 のとき en2pπi=en2qπi である。
すなわち {en2kπi∣k=0,1,⋯,n−1} は相異なる。
- 逆に xn=1 の解が en2kπi でつくされること
代数学の基本定理より,xn−1=0 は複素数の範囲で(重複度を含めて)n 個の解を持つ。よって 1 の n 乗根は高々 n 個存在する。
前半より {en2kπi∣k=0,1,⋯,n−1}
は相異なる n 個の集合
である。
よって en2kπi の他に xn=1 の解は存在しない。
補足
0<k<n のとき en2kπi=1 であることを示します。
0<k<n より 0<n2kπ<2π となります。
このとき cosn2kπ=1 です。
en2kπi=cosn2kπ+isinn2kπ であったため,en2kπi の実部が 1 にならないことが従います。
こうして en2kπi=1 であることが従います。
因数定理をうまく使うことで,簡単な計算により解が相異なることを示すことができます。
相異なるn個の解を持つことの別証明
f(x)=xn−1 とおく
xn=1 の解は,f(x)=0 の解と解釈することができる。
f′(x)=nxn−1 である。この解は x=0 であるが,f(0)=−1=0 である。
こうして f(x)=0 と f′(x)=0 は共通解を持たない。
よって因数定理の重解バージョンより f(x)=0 は重解を持たないから,その解は相異なる。
複素数の n 乗根
2 の2乗根は 2,−2 でした。これは 2⋅(±1) と理解できます。
このように一般の n 乗根は,1 の n 乗根を用いて表すことができます。
定理
a を 0 でない複素数,n を 1 以上の整数とする。
a の n 乗根は複素数の範囲でちょうど n 個存在し,
rn1eni(θ+2kπ)(k=0,1,2,…,n−1)
と表される。
ただし,r=∣a∣,θ=arga である。
定理の中の r1/n は正の実数の場合における r>0 の n 乗根のことです。
rn1eniθen2kπi と考えてもよいです。rn1eniθ は a の n 乗根の1つであり,それを 1 の n 乗根で「ズラしていく」と考えることもできます。
例
- 25 の2乗根は 5,−5 の2個
- 64 の3乗根は ω=2−1+3i として 4,4ω,4ω2 の3個
- −3 の2乗根は 3i,−3i の2個
証明
{r1/nei(θ+2kπ)/n} は xn=a の解を与える。実際
(r1/nei(θ+2kπ)/n)n=rei(θ+2kπ)=reiθ=a
と計算される。
これらが相異なることは,1 の n 乗根における議論で示されている。
代数学の基本定理より xn=a が n 個の解を持つことと合わせることで,{r1/nei(θ+2kπ)/n} は a の n 乗根を与えることが示される。
補足と例題
しばしば en2πi=ζn と書くことがあります。
-
a が正の実数のとき,複素数の範囲の a の n 乗根は
a1/n,a1/nζn,…,a1/nζnn−1
の n 個となります。
-
複素数の積を扱う時は極形式を考えて「絶対値は積,偏角は和」になることを使うと見通しがよくなることが多いです。→複素数平面における極形式と回転
例題
例題
- ζn=en2πi とおく。ζn+ζn2+⋯+ζnn−1 を求めよ。
- cosn2π+cosn4π+⋯+cosn2(n−1)π を求めよ。
- sinn2π+sinn4π+⋯+sinn2(n−1)π を求めよ。
ζnk が xn−1=0 の解であることを利用をして解いてみましょう。
解
-
1,ζn,ζn2,⋯,ζnn−1 は それぞれ相異なる 1 の n 乗根である。すなわち相異なる n 個の xn−1 の解である。
n次方程式の解と係数の関係 より ζn+ζn2+⋯+ζnn−1 は xn−1 の係数と一致する。よって
1+ζn+ζn2+⋯+ζnn−1=0
である。
1 を移項して
ζn+ζn2+⋯+ζnn−1=−1
を得る。
-
ζn=cosn2π+isinn2π であるため,ζn+ζn2+⋯+ζnn−1 の実部を見ることで
cosn2π+cosn4π+⋯+cosn2(n−1)π=−1
を得る。
-
2 同様にして
sinn2π+sinn4π+⋯+sinn2(n−1)π=0
である。
一方で ζn+ζn2+⋯+ζnn−1 が等比数列であることを用いて計算をすることができます。
別解
-
等比数列の和の公式を用いることで
ζn+ζn2+⋯+ζnn−1=ζn⋅1−ζn1−ζnn−1=1−ζnζn−ζnn=1−ζnζn−1=−1
となる。
-
同様
-
同様
他に 1 の n 乗根を活用する問題として
入試数学コンテスト第5回第6問解答解説
も是非見てください。










