開平法のやり方と原理
更新
筆算を用いてルートを計算する「開平法」を紹介します。
の近似値を求める例を見てみましょう。
難しいのは手順4だけです!
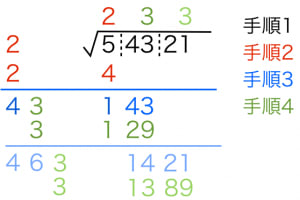
-
まず と右側に書く。小数点を基準に2桁ずつ区切っていく。
-
二乗して「右側の最も左のブロック(この例だと )」以下となるような最大の整数(この場合 )を求める。その数を右側に1箇所,左側に2箇所書く。また,計算結果(この場合 )を右側に書く。
-
左側は足し算,右側は引き算。
-
左側の数(この場合 )の末尾に をくっつけたもの が右側の次のブロックまで取ったもの(この場合 )以下となるような最大の整数を求める。その数を右側に1箇所,左側に2箇所書く。この場合, であり, が該当する。また,その計算結果(この場合 )を右側に書く。
-
以下,3と4を必要なだけ繰り返す。
の近似値が と求まりました。実際, です。
なお,筆算を用いない方法もあります。→ルートの近似値を計算する素朴な方法とコツ
開平法で小数点以下も計算
開平法で小数点以下も計算

小数点以下も同様に計算できます。
ルート2の近似値計算を筆算で行った例を図に示します。
と見て,小数点を基準に2桁ずつ区切っていきます。
の近似値が と求まりました。計算結果の小数点の位置にも注意してください。
開平法の原理
開平法の原理
開平法で何をやっているのか,大雑把に説明します。証明というほどたいそうなものではありませんが,雰囲気はつかめると思います。
の近似値を開平法で求めたいとします。
まず,手順1と手順2で の上1桁を計算している。 の桁数が(小数点を基準にして)偶数なのか奇数なのかによって挙動が変わることに注意。
そして「 はだいたい 」という下からの評価が得られる。
(上の例だと, はだいたい , はだいたい という評価)
しかし,本当は であるとする。 を求めたい。
上式を変形すると,
よって, が をこえないようなもの を使って,評価を「 はだいたい 」と更新する(上の例だと, はだいたい , はだいたい という評価)。手順3,4における左側の数字が ,右側の数字が に対応している。
改めて,本当は であるとする。 を求めたい。
上式を変形すると, よって, が をこえないようなもの を使って,評価を「 はだいたい 」と更新する。
これを繰り返す。
図がカラーであることの強みを発揮できた記事だと思います。











