複素数の絶対値の定義といろいろな性質

更新日時 2023/07/26

複素数の絶対値

複素数 $z=a+bi$ の絶対値 $|z|$ を $|z|=\sqrt{a^2+b^2}$ で定める。

複素数の絶対値について整理しました。

複素数の絶対値とは

複素数 $z=a+bi$ の絶対値 $|z|$ の定義は $|z|=\sqrt{a^2+b^2}$ です。

例

$3+4i$ という複素数の絶対値は $|3+4i|=\sqrt{3^2+4^2}=5$

特に， $b=0$ の場合は $|z|=\sqrt{a^2}=|a|$ となります。つまり，慣れ親しんでいる実数の絶対値と一致します。

例

$2$ という複素数の絶対値は $|2|=2$

複素数の絶対値は定義より必ず実数です。

複素数平面と絶対値

複素数の絶対値は複素数平面における原点からの距離を表すとも言えます。
（三平方の定理より
(0,0)(0,0)(0,0)
 と
(a,b)(a,b)(a,b)
 の距離は
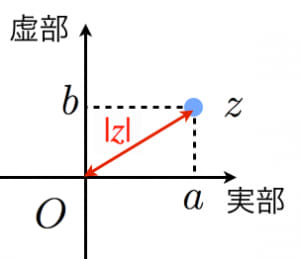
a2+b2\sqrt{a^2+b^2}a2+b2​
 であるためです）
実数の絶対値は「数直線における原点からの距離」
複素数の絶対値は「複素数平面における原点からの距離」

絶対値の非負性

ここから複素数の絶対値の性質をたくさん紹介します。

以下， $z,w$ は複素数とし， $z=a+bi,\:w=c+di$ とします（ $a,b,c,d$ は実数）。

絶対値の非負性

$|z|\geqq 0$
$|z|=0\iff z=0$

前半の証明： $\sqrt{a^2+b^2}\geqq 0$ より成立
後半の証明： $\sqrt{a^2+b^2}=0\iff a=0,b=0$ より成立

絶対値と三角不等式

ここからは「四則演算＋絶対値」に関する性質です。

まず，和と差については三角不等式が成立します。

三角不等式

$|z+w|\leqq |z|+|w|$
$|z-w|\geqq |z|-|w|$
$|z+w|\geqq |z|-|w|$

いろいろな三角不等式（絶対値，複素数，ベクトル）で証明しています。

絶対値の積と商

絶対値の積

$|zw|=|z||w|$

特に， $z$ が実数の場合が頻出です。例えば $|2z|=2|z|$ です。

証明

単純計算で証明できる。

$\begin{aligned} &|zw|\\ &=|(a+bi)(c+di)|\\ &=|(ac-bd)+(ad+bc)i|\\ &=\sqrt{(ac-bd)^2+(ad+bc)^2}\\ &|z||w|\\ &=|a+bi||c+di|\\ &=\sqrt{a^2+b^2}\sqrt{c^2+d^2} \end{aligned}$

より， $(ac-bd)^2+(ad+bc)^2=(a^2+b^2)(c^2+d^2)$ を証明すればよいが，これは簡単に確認できる（実は有名な恒等式→ラグランジュの恒等式とその仲間）。

絶対値の商

$\left|\dfrac{z}{w}\right|=\dfrac{|z|}{|w|}$ （ただし $w\neq 0$ ）

特に， $z=1$ の場合が重要です（逆数の絶対値の公式）。

証明

分母の実数化を用いて証明できる。

$\begin{aligned} \left|\dfrac{z}{w}\right| &=\left|\dfrac{a+bi}{c+di}\right|\\ &=\left|\dfrac{(a+bi)(c-di)}{c^2+d^2}\right| \end{aligned}$

より，

$\dfrac{\sqrt{(ac+bd)^2+(-ad+bc)^2}}{c^2+d^2}=\dfrac{\sqrt{a^2+b^2}}{\sqrt{c^2+d^2}}$ を証明すればよいが，結局積の公式と同じ恒等式に帰着される。

また，積の公式でで $z\to\dfrac{z}{w}$ としても下側が導けます。

共役複素数と絶対値

$z$ の共役複素数 $a-bi$ を $\overline{z}$ と書きます。

$|z|=|\overline{z}|$
$z\overline{z}=|z|^2$

上側は $\sqrt{a^2+b^2}=\sqrt{a^2+(-b)^2}$ から導けます。
下側は $(a+bi)(a-bi)=a^2+b^2$ から分かります。非常に重要な性質です。→共役複素数の覚えておくべき性質
$\overline{z}=\dfrac{|z|^2}{z}$ の形で使うことも多いです，