ラグランジュの恒等式とその仲間

更新日時 2023/07/26

有名な恒等式たちについて解説します。

ブラーマグプタ-フィボナッチ恒等式（BF恒等式）
$(a^2+b^2)(c^2+d^2)\\ =(ac-bd)^2+(ad+bc)^2\\ =(ac+bd)^2+(ad-bc)^2$
ブラーマグプタの恒等式
$(a^2+nb^2)(c^2+nd^2)\\ =(ac-nbd)^2+n(ad+bc)^2\\ =(ac+nbd)^2+n(ad-bc)^2$
ラグランジュの恒等式
$\displaystyle \left( \sum_{i=1}^na_i^2 \right) \left( \sum_{i=1}^nb_i^2 \right)\\ =\displaystyle \left( \sum_{i=1}^na_ib_i \right)^2 + \sum_{1\leq i < j \leq n} ( a_ib_j-a_jb_i )^2$
ビネ-コーシーの恒等式
$\displaystyle \left( \sum_{i=1}^n a_i c_i \right) \left( \sum_{i=1}^n b_i d_i \right)\\ =\displaystyle \left( \sum_{i=1}^n a_i d_i \right) \left( \sum_{i=1}^n b_i c_i \right)\\ \quad \displaystyle + \sum_{1\leq i < j \leq n} (a_i b_j - a_j b_i ) (c_i d_j - c_j d_i)$

ラグランジュの恒等式とビネコーシーの恒等式は，シグマのせいでごちゃごちゃしているように見えますが，実は非常に美しい恒等式です。

以上の恒等式は全て有名なので，なんとなく頭の片隅にとどめておきましょう，覚えるならブラーマグプタとラグランジュがおすすめです。

恒等式たちの関係

恒等式の関係

ブラーマグプタの恒等式で $n=1$ としたものがBF恒等式です。
ラグランジュの恒等式で $n=2$ としたものがBF恒等式です。
ビネ-コーシーの恒等式で $a_i=c_i, b_i=d_i$ としたものがラグランジュの恒等式です。
ビネ-コーシーの恒等式を行列に拡張したビネ-コーシーの定理というのがあります。以上をまとめると図のようになります。
BF恒等式を拡張したオイラーの4平方恒等式というものもあります。

恒等式の証明

BF恒等式やブラーマグプタの恒等式は，右辺を展開して左辺と一致することがすぐに確認できます。

上述した包含関係より，ビネ-コーシーの恒等式を証明すればラグランジュの恒等式も証明されるので，ビネ-コーシーの恒等式を証明します。

証明

$\begin{aligned} &\sum_{1\leq i < j \leq n} (a_ib_j-a_jb_i) (c_id_j-c_jd_i)\\ &= \sum_{1\leq i < j \leq n} (a_i b_j c_i d_j + a_j b_i c_j d_i) + \sum_{i=1}^n a_i b_i c_i d_i\\ & \:\: - \sum_{1\leq i < j \leq n} (a_i b_j c_j d_i + a_j b_i c_i d_j) - \sum_{i=1}^n a_i b_i c_i d_i\\ &=\sum_{i=1}^n \sum_{j=1}^n a_ib_jc_id_j - \sum_{i=1}^n \sum_{j=1}^n a_ib_jc_jd_i\\ &= \left( \sum_{i=1}^na_ic_i \right) \left( \sum_{i=1}^nb_id_i \right) - \left( \sum_{i=1}^na_id_i \right) \left( \sum_{i=1}^nb_ic_i \right) \end{aligned}$

2行目への式変形の際に同じものを足して引きました（第2項と第4項）。
4行目への変形は少しわかりにくいので，イメージを図に示します。 (赤＋青)＋緑＝全体です。
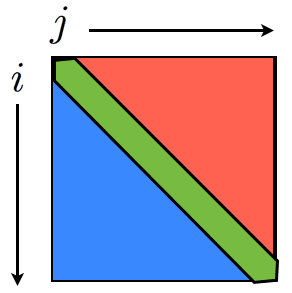
最終行への変形の際にシグマの分解を用いました。(→シグマ計算を機械的に行うための3つの公式)

恒等式の応用

1. シュワルツの不等式の証明
ラグランジュの恒等式から，∑i=1nai2∑i=1nbi2≥(∑i=1naibi)2\displaystyle\sum_{i=1}^na_i^2\sum_{i=1}^nb_i^2 \geq (\sum_{i=1}^na_ib_i)^2i=1∑n​ai2​i=1∑n​bi2​≥(i=1∑n​ai​bi​)2
 が一瞬でわかるので，ラグランジュの恒等式はシュワルツの不等式の証明そのものになっています。
2. ペル方程式への応用
x2−ny2=1x^2-ny^2=1x2−ny2=1
 をペル方程式と言い，ペル方程式の整数解を求める問題が広く研究されています。→ペル方程式に関する基本的な性質まとめ
ペル方程式の整数解
(x1,y1), (x2,y2)(x_1,y_1),\:(x_2, y_2)(x1​,y1​),(x2​,y2​)
  (同じものでもよい)が見つかれば，ブラーマグプタの恒等式で
a=x1, b=y1, c=x2, d=y2, n=−na=x_1,\:b=y_1,\:c=x_2,\:d=y_2,\:n=-na=x1​,b=y1​,c=x2​,d=y2​,n=−n
 として，
(x1x2−ny1y2)2−n(x1y2−y1x2)2=1
(x_1x_2-ny_1y_2)^2-n(x_1y_2-y_1x_2)^2=1
(x1​x2​−ny1​y2​)2−n(x1​y2​−y1​x2​)2=1
となるので，(x1x2−ny1y2,x1y2−y1x2)(x_1x_2-ny_1y_2,x_1y_2-y_1x_2)(x1​x2​−ny1​y2​,x1​y2​−y1​x2​)
 もペル方程式の解であることが分かります。
こうして，
2つ（または1つ）の整数解から無数の整数解を生成できます。
3. フェルマーの二平方和定理の証明
フェルマーの二平方和定理とは，整数 nnn がいつ平方数の和になるかがわかる定理です。この証明にはブラーマグプタの恒等式を用います。
詳しくは フェルマーの二平方和定理 をご覧ください。
私の好きな恒等式はラグランジュの恒等式です！