分散の意味と2通りの求め方・計算例
分散とは,データの「バラつきの大きさ」「散らばりの大きさ」を表す指標。
- 分散が大きい → バラつきが大きい,平均から遠いものが多い
- 分散が小さい → バラつきが小さい,全部が平均に近い,まとまっている
分散の意味 や 分散の定義式の理由,分散をすばやく計算する方法 について解説します。
分散の定義と計算例
分散の定義と計算例
分散とは,「平均からの差」の二乗の平均のこと。式で書くと,分散は ただし, はデータの数で, は各データの値, は平均です。
つまり,分散は以下の3ステップで計算できます。
- 「平均 」を計算する
- 「平均からの差の二乗 」を計算する
- その結果の平均を計算する
具体例で分散を計算してみましょう。
というデータに対して分散を計算せよ。
手順1. 平均を計算
手順2.「平均からの差の二乗」を計算
それぞれのデータと の差の二乗を計算する:
手順3. 計算結果の平均を計算
つまり,分散は になります。
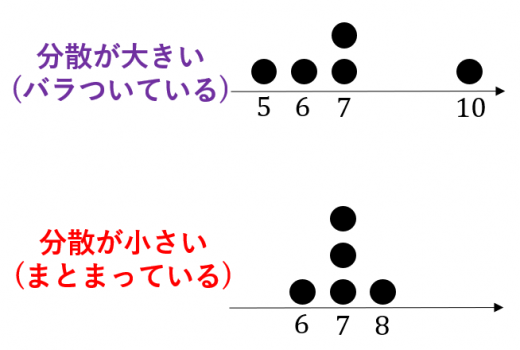
分散の意味
分散の意味
「5人のテストの点数(10点満点)」について,以下の2つの状況を考えてみます。
- 状況1: テストの点数がそれぞれ
- 状況2: テストの点数がそれぞれ
どちらも平均点を計算してみると 点になります。しかし,
- 状況1は「点数が比較的バラバラ」
- 状況2は「全員が平均点に近い」
と言えます。このように,平均点が同じでも「データがどれくらいバラついているか」によって,状況が変わります。分散は「データがどれくらいバラついているか」を数値で表したものです。実際,状況1の分散は で状況2の分散は になります。
分散の記号・呼び方
分散の記号・呼び方
-
分散は という記号で表されることが多いです。
-
分散は英語で Variance なので,確率変数 の分散を や で表すことが多いです。
-
分散は の期待値なので と表すこともあります。分散は,平均まわりの二次モーメントと呼ばれることもあります。
-
分散の式に登場する のこと(平均との差のこと)を偏差と言います。
分散をすばやく計算する方法
分散をすばやく計算する方法
分散は 「二乗の平均」 と 「平均の二乗」 の差で計算できる。つまり,分散 は となる。
最初の例題について,こちらの方法で計算してみます。
の分散を求めよ。
-
平均は なので 「平均の二乗」 は
-
一方 「二乗の平均」 は
-
よって,分散は 「二乗の平均」 と 「平均の二乗」 の差なので
さっきと同じ答えになりました!
分散の計算方法を2つ紹介しました:
- 方法1: 分散の定義から計算。つまり「平均からの差の二乗」の平均
- 方法2. 「二乗の平均」と「平均の二乗」の差,という公式で計算。
今回の例では,どちらの計算方法でも手間はあまり変わりませんが,平均値がキリの悪い数のときは2番目の方法が楽なことも多いです。少なくとも検算にはなります(エクセルなどの関数で計算するなら関係ありませんが)。
分散をすばやく計算する方法の証明
分散をすばやく計算する方法の証明
分散が 「二乗の平均」 と 「平均の二乗」 の差で計算できることを証明しておきます。
などの値は直接用いずに,期待値のまま計算していきます。
ちなみにこの定理と証明について,似たようなものが共分散にも存在します。→共分散の意味と簡単な求め方
分散の式の理由
分散の式の理由
分散はデータのバラつき具合を表す指標ですが,なぜ という式で定義されるのでしょうか?
理由
データ が平均 から離れているほど は大きくなるので,上の式で分散を定義すれば 「バラつきが大きいほど分散が大きくなる」と言えます。つまり,データのバラつき具合を表す指標になります。
バラつき具合を表す指標は他にもある
分散の定義は偏差の二乗和の平均ですが「二乗」であることに絶対的な意味はありません。例えば,
という式で定義される絶対値平均誤差という指標もあります(絶対値をつけないと必ず0になり意味のある指標にはなりません)。
ただし,多くの確率分布に対して分散の計算は楽(綺麗な形で求まる)なので分散が広く使われています。
また,単位の次元をそろえるために 分散の平方根を取った標準偏差 が用いられることも多いです:
私は日常会話でも「当たり外れが大きい」という意味で「分散」という言葉をけっこう使います。










