破産の確率と漸化式
漸化式を用いて確率を求める有名問題を解説します。
- 難関大の受験対策のよい練習になります。
- 現実的でおもしろい話題です。
破産の確率の問題
破産の確率の問題
以下の問題を考えます。
円持っている。勝ったら 円もらえ,負けたら 円失う勝負を繰り返し行う。勝つ確率は である。 円になったら十分儲かったとみなして勝負は終了する。このとき所持金が 円になって終了する確率(破産する確率)を求めよ。
数学で扱いやすいように問題を言い換えます。
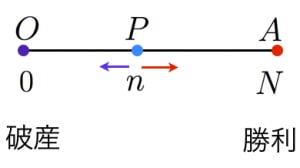
数直線上に がある()。
は動点であり「確率 で正の方向に1進み,確率 で負の方向に1進む」という行動を繰り返す。 が か にたどり着いたら終了。このとき にたどり着いて終了する確率はいくらか?
結果と考察
結果と考察
答えがおもしろいので,導出の前に結果を書いてしまいます!
破産確率は,
のとき
のとき
ただし,表記簡略化のために とおきました( が大きいほど負ける確率が高い)。
破産確率についての考察
- のときの結果が非常に美しいです。特に のとき,当然ですが破産確率は になります。
- を固定すると破産確率は の減少関数になっています。これは,スタートの位置が「破産側」より「勝利側」に近いほど破産確率が低いという直感とも合致します。
- のとき, です。 と が十分大きいとき(例えば )破産確率はほぼ です。
- のとき, です。 が十分大きく, がさらに十分大きいとき(例えば )破産確率はほぼ です。
つまり,たくさんの回数勝負する場合は勝率が より大きいかどうかによって「ほぼ確実に勝てる」か「ほぼ確実に破産する」かが決まります。
破産確率の導出
破産確率の導出
ここからは破産確率を導出していきます。
まずは重要な漸化式を立てる部分です。
を固定して を変数だと考える。破産の確率は の関数である。その確率を とおく。
破産の確率を一回目に勝つ場合と負ける場合に分けて考えることにより,以下の漸化式を得る:
(一回目に勝てばその後確率 で破産,一回目に負ければその後確率 で破産)
ただし,端っこ()でも漸化式が成立するように とする。
あとはこの三項間漸化式を解くだけです。どの方法でもOKですが,今回は三項間漸化式の3通りの解き方の二つ目の解き方を使います。
多くの三項間漸化式では初期条件が で与えられるのに対して,今回は と で与えられていることに注意してください。
特性方程式は であり,この解は と である。 のときは重解となるので場合分けが必要。
・ のとき,
漸化式の解は と書ける。
を満たすように を決めると, となる:
・ のとき,
漸化式の解は と書ける。
を満たすように を決めると, となる:
なお, のときは電気回路との対応定理を使えば一瞬で解けます。
破産したくないなら勝率が0.5より確実に大きい賭けを探さないといけません。











