テント写像とその性質〜東大入試の背景〜
をパラメータとして,
と表される関数(写像)をテント写像と言う。
東大後期入試のテーマにもなった の場合のテント写像について考察します。
テント写像
テント写像
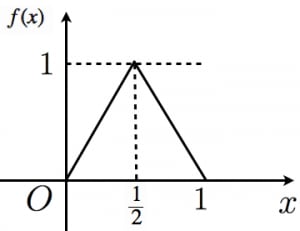
今回考える関数は, 上で定義された以下のような関数です。
グラフは図のようになります。この形がテントっぽいのでテント写像と言います。
合成
合成
次に のグラフについて考えてみます。
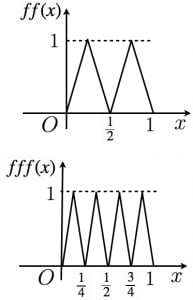
の範囲で の値は の値に比例して から まで増加します。よって, の値は まで増加してそこから減少します。
についても同様に考えることで のグラフは図のようになることが分かります。
同様に, のグラフはテントが つあるようなグラフになります。
さらに一般に, を 個合成した関数 はテントが 個あるようなグラフになります。
初期値鋭敏性
初期値鋭敏性
さきほど見たように は激しく( に関して指数的に)ギザギザしています。
そのため, の値は を少し変えただけでも大きく変わってしまいます。このような性質を初期値鋭敏性と言います。
初期値鋭敏性はカオス力学系と呼ばれるものの一つの性質(定義)です。「カオス」という数学の分野があるくらい深い話題です。
周期点
周期点
関数 を何回か作用させると元に戻ってくる点を周期点と言います。
周期点の集合は, 全ての正の整数 に対して, の解(固定点,不動点)を集めたものです。
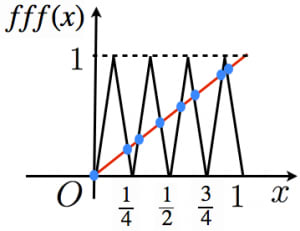
そこで について考えてみます。これは と の交点に対応するので,さきほど書いたグラフより全部で 個あることが分かります。
よって,周期点は無限個あることも分かります。
東大の問題との関連
東大の問題との関連
-
2002年東大後期第3問はテント写像を題材とした問題でした。
(5)まであり,(1)から(3)までは のグラフが書ければ解けたも同然の問題。(4),(5)はやや難しいですが,テント写像の話題を知っていればかなり有利です(マニアックなテーマなのでほとんどの受験生が知らなかったと思いますが)。 -
のグラフから合成関数 のグラフをイメージするのは重要な考え方です。2004年東大文系第3問,理系第4問はこの考え方を知っていれば一瞬で解ける問題でした。
JMOの予選を受けた方,お疲れ様でした!











