全射の個数の証明とベル数
場合の数に関する3つの公式を紹介します。見た目は複雑ですが,1が理解できれば2,3は難しくありません。順番に解説します。
-
全射の個数の公式:
人を区別のある(ちょうど) 個のグループに分ける場合の数は,
-
スターリング数の公式:
人を区別のない(ちょうど) 個のグループに分ける場合の数(スターリング数)は,
-
ベル数の公式:
人を区別のない 個以下のグループに分ける場合の数(ベル数)は,
全射の個数の例
全射の個数の例
まずは, 人を区別のある(ちょうど) 個のグループに分ける場合の数を考えます。もちろん人間は区別します。つまり,今回は「区別するもの」を「区別するグループ」に分ける場合の数の問題です。
具体例として でやってみます。
人をチームA,チームK,チームBに分ける場合の数を求めよ。ただし,各チーム最低1人はメンバーが属するものとする。
1: 人を チーム以下に分ける場合の数は, 通り。
2:そのうち,「チームAに誰も属さない」or「チームKに誰も属さない」or「チームBに誰も属さない」場合の数を除けばよい。
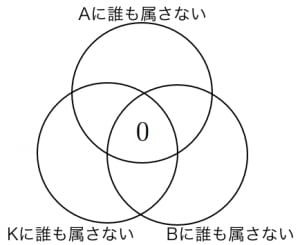
2についてはベン図を描けば分かりやすい,Aに誰も属さない場合の数は 通り, にも にも誰も属さない場合の数は 通り,いずれも誰も属さない場合の数は 通りであることに注意する。よって,2の場合の数は,
と分かる。
よって,求める場合の数は,
通り。
全射の個数の証明(一般の場合)
全射の個数の証明(一般の場合)
上記の例題を一般化すると公式1が証明できます。
人を区別のある(ちょうど)
個のグループに分ける場合の数は,
ただし,グループの数が つ以上の場合はベン図を描くことができないので,難易度が上がります。この場合は包除原理を用います。→包除原理の2通りの証明
人を チーム以下に分ける場合の数は 通り。
このうち,いずれかのチームに誰も属さないような場合の数を除けばよい。これは包除原理より,
となる。これを後ろから足し合わせる:
よって,求める場合の数は,
最短で得点力を上げる!高校数学の問題集〈典型250問〉の問題151では, の場合の問題と2通りの解法を紹介しています。
スターリング数を求める
スターリング数を求める
人を区別のないちょうど 個のグループに分ける方法の数をスターリング数といい, などと書きます。→スターリング数の漸化式と3つの意味
全射の個数の公式を用いることで,スターリング数をシグマと二項係数で表すことができます!
定義により,「区別のない場合」のスターリング数は「区別のある場合」の全射の個数の公式を で割ったものなので,
となります。
ベル数を求める
ベル数を求める
人を区別のない 個以下のグループに分ける方法の数をベル数といい, などと書きます。
スターリング数の公式を用いることで,ベル数をシグマと二項係数で表すことができます!
定義により なので,
なお,3つの公式を覚える必要はありませんが,導出できるようになっておきましょう。 なら大学入試として適度な難易度です。
区別するのかしないのか,きちんと区別しましょう。











