対称式について覚えておくべき7つの公式
更新
対称式とは,どの2つの変数を交換しても変わらない多項式のことです。
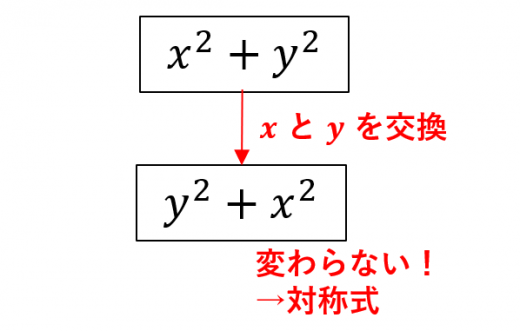 例えば, という式で と を交換すると になります。 なので多項式として変わっていません。よって は対称式です。
例えば, という式で と を交換すると になります。 なので多項式として変わっていません。よって は対称式です。
対称式に関する重要な7つの公式と例題を解説します。
2変数の対称式に関する基本公式と例題
2変数の対称式に関する基本公式と例題
, のとき, の値を求めよ。
公式1を使うと,
補足:このように と の対称式は と の多項式で表せます! と のことを基本対称式と言います。
のとき, の値を求めよ。
として公式2を使うと,
n乗の和を基本対称式で表す
n乗の和を基本対称式で表す
, のとき の値を求めよ。
公式3を使って の値を, から順々に求めていく。
- 例題1で求めたように,
- 公式3より,
- 公式3より,
補足:
- このように, の場合が求まれば の場合の が求まります。
- 程度なら以下のように普通に計算してもよいです:
- 以下の計算が一番スマートです:
引き算も対称式で表せる場合がある
引き算も対称式で表せる場合がある
は対称式ではありませんが,公式4を使って と の値から の値を計算できます。頻出です。
上の4つの公式はすべて非常に重要です。
なお,2変数の対称式についてのさらに詳しい解説は →2変数の対称式と基本対称式の4つの性質
三変数の対称式を基本対称式で表す
三変数の対称式を基本対称式で表す
の対称式は と と の多項式で表せる。
三変数 に関しての基本対称式は の つです。全ての対称式は で表すことができるのです。
例えば,
- 公式5:
- 公式6:
のように,すべての対称式が の多項式で表せます。公式5は
の展開公式を移項するだけで簡単に導出できます。公式6は因数分解公式を用いれば簡単に導出できます!→因数分解公式一覧
具体的には,
の右辺第二項に公式5を用いて整理すると導出できます。
また, を基本対称式で表す際に使えるのが,
- 公式7:
です。ただし, とおきました。
公式7は公式3の三変数バージョンです。入試レベルではほとんど必要にならない公式なので面白いなあと思うくらいで軽く流しておいてください。数学オリンピックレベルだとたまに活躍します。
対称式の基本定理
対称式の基本定理
この記事では,以下の2つの定理を紹介しました。
- と の対称式は と の多項式で表せる。
- の対称式は と と の多項式で表せる。
より一般的な定理として,全ての対称式は基本対称式で表せるというものがあります。これを対称式の基本定理と言います。詳しくは対称式の基本定理とその証明を参照してください。
対称なものはできるだけ対称なまま変形したいですね。










