安定マッチングとGale-Shapleyアルゴリズム

今回考えるのは安定結婚問題と呼ばれる問題です。

$n$ 人の男性と $n$ 人の女性がいて，各人の異性に対する希望順位が与えられた状況を考えます。全員が「それなりに幸せになれる」ような結婚のペアの決め方（完全マッチング）を求めるのが目標です。

安定結婚問題では 「全員がそれなりに幸せになれる」→「かけおちするペアが発生しない」と考えます。

「かけおちするペア」とは，夫婦でない二人組で，お互い今の相手よりも希望順位が高いペアです。不安定対と言います。

例えば，さきほどの例において緑の線 $(A,c),(B,b),(C,a)$ をペアにしてみます。このとき $(B,c)$ が不安定対となります。なぜなら $B$ は今の相手 $b$ よりも新しい相手候補 $c$ の方が順位が高く，$c$ も今の相手 $A$ よりも新しい相手候補 $B$ の方が順位が高いため，かけおちしたいと思ってしまうからです。

不安定対が存在しないような完全マッチングのことを，安定マッチングと言います。安定マッチングを機械的に見つけてくれるのがGale-Shapley（ゲール-シャプレー）アルゴリズムです。

以下の具体例も参照しながら理解してみてください！

1. 誰にもキープされていない男性1人が，（今までふられていない中で）一番結婚したい女性に告白する。

2. 告白を受けた女性は
   受理パターン：相手がいない or 今キープしている人よりもよい相手なら告白してきた人をキープにする（今までキープしてた人とはさよならする）
   拒否パターン：今キープしている人の方がよいなら告白を断る。

1，2を何回も繰り返し，全男性が誰かしらにキープされたらその時点のペア（完全マッチング）を取ってくる。これによって安定マッチングが得られる！

さきほどの例でGale-Shapleyをやってみます。

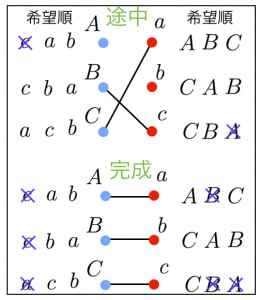
• Aがcに告白，cは相手がいないので受理（キープ）
• Bがcに告白，cはキープしてるAよりもBのがよいのでAをふってBをキープ
• Cがaに告白，aは相手がいないので受理

（ここまで経過した状態が上側の図）

• Aは第一希望にふられたので第二希望のaに告白，aはキープしてるCよりもAのがよいのでCをふってAをキープ
• Cがcに告白，cはキープしてるBよりもCのがよいのでBをふってCをキープ
• Bがbに告白，bは相手がいないので受理（Bで妥協）

全男性が誰かにキープされたのでここで終了。安定マッチングが得られた。

ゲールシャプレーで安定マッチングが得られることの証明は省略します。背理法で証明できますのでやってみてください。

• お互い1位どうしに希望すれば，そのペアは必ず安定マッチングに含まれます。
• Gale-Shapleyの計算量は $O(n^2)$ です。効率的に安定マッチングが計算できます！
• （男性が告白するタイプの）Gale-Shapleyアルゴリズムにおいて，出力される安定マッチングは，男性がどのような順番で告白するかによりません。
• 役割を交換して，女性側が告白し男性側がキープするタイプのアルゴリズムも考えることができます。男性告白タイプ，女性告白タイプ，どちらを使っても安定マッチングを得ることはできますが，（一般には）異なる安定マッチングが得られます。
• 似て非なる話題としてHallの結婚定理というものがあります。→Hallの結婚定理とその証明

Tag:数学の定理No.1決定戦