Hallの結婚定理とその証明
Hall(ホール)の結婚定理:頂点集合が と分割された二部グラフ に対して,以下は同値。
条件1: の頂点を全てカバーするマッチングが存在する
条件2(Hallの条件):任意の の部分集合 に対して,
ただし, は と辺でつながっている頂点の集合。
ホールの定理,結婚定理とも。グラフ理論の言葉で書くと一見分かりにくいですが,意味が理解できると非常に面白い定理です。
マッチングとは
マッチングとは
まず,条件1を理解するためにマッチングについて説明します。
(追記:二部グラフの最大マッチングと増加道)
マッチングとは端点がかぶらないように辺をいくつか取ってきたものです。また,マッチングの端点に属する頂点を「マッチングでカバーされている」と言います。
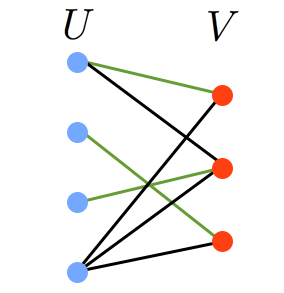
例えば,図では緑の辺がマッチングの一例です。頂点集合 の中で上三つはカバーされていますが,一番下はカバーされていません。 は全てカバーされています。
の各頂点を男性, の各頂点を女性,男性 が女性 とお互いに結婚してもよいと思うとき に辺を引いたグラフを考えてみます。このときマッチングは結婚成立の一例を表しています。
すなわち条件1は, 「うまいマッチングを選べば男がみんな結婚できる」という条件になります。
結婚条件(Hallの条件)について
結婚条件(Hallの条件)について
次は条件2について説明します。 の部分集合 に対して, とは と辺でつながっている頂点の集合で, の部分集合です。
例えば,図において などです。

日本語で言うと,男を適当に何人か選んだとき,その男たちと結婚しうる女性を寄せ集めてきた集合です。
すなわち条件2は 「男を適当に何人か選んでくると,その男たちと結婚しうる女性の人数の方が多い」という条件になります。
例えば,図では とすると となっているのでHallの条件を満たしていません。これでは の誰かは明らかに結婚できません。
ここまで理解できればHallの定理における「条件1→条件2」は簡単に証明できます。
対偶を示す。条件2が成立しないとき,ある の部分集合 が存在して, となる。
よって, をカバーするようなマッチングは存在せず,条件1は成り立たない。
つまり,Hallの条件は をカバーするマッチングが存在するための必要条件というわけです。実はこれが十分条件にもなっているというのがHallの結婚定理の偉大なところです。驚きですね!
Hallの結婚定理の証明
Hallの結婚定理の証明
それではいよいよ難しい方:「条件2→条件1」を帰納法で証明します。少し長いですが見かけほど難しくありません。
に関する帰納法で証明する。 のときは自明。
のときにHallの結婚定理が成立すると仮定する。 でありHallの条件を満たすグラフ でを考える。以下二通りに場合分け。
・ の任意の真部分集合 に対して となる場合。
このときは余裕があるので,適当に辺 を一本選べばよい。そして,頂点 と を除いた二部グラフ を考えると, においてもHallの条件を満たしている。よって,帰納法の仮定により をカバーするマッチング が存在する。全体のマッチングとして と の和集合を持ってくればよい。
・ を満たす の真部分集合 が存在する場合。
「 と から構成される二部グラフ」がHallの条件を満たしていることと,帰納法の仮定により,頂点 をカバーするマッチング が存在する。そして,そのマッチングは と の間の完全マッチング(全頂点をカバーするマッチング)である。
よって,残ったグラフ に をカバーするマッチング が存在することを証明すればよい。

ここで, の部分集合 を考えてみると, がHallの条件を満たしていることから である。よって, の行き先で に属さないものが少なくとも 個は存在する。それらは とはつながっていないので,全て とつながっている。すなわち, 。よって. もHallの条件を満たすので帰納法の仮定により をカバーするマッチング が存在する。
ちなみに,マッチングは二部グラフ以外の一般のグラフでも考えることができます。一般グラフではHallの定理の拡張としてTutteの定理というものがあります。
マッチングの理論は非常に美しいです。最高です。











