懸垂線の２通りの導出

長いひもの一部 $0\leq x \leq x_0$ の区間を考える。両端にかかる張力を $T_0, T$，ひもにかかる重力を $W$，$x_0$ でのひもの角度を $\theta$ とおく。

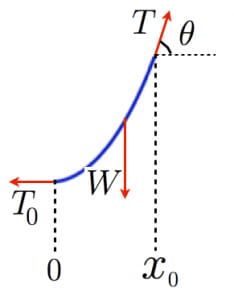
$T_0$ は $x_0$ によらない定数なので（注），力の釣り合いから以下の式が成立する：

$T\cos\theta=T_0, T\sin\theta=W$

よって，$\tan\theta=\dfrac{W}{T_0}$

ここで，$W$ は線の長さ $s$ に比例するので，

$\dfrac{dy}{dx}=\tan\theta=\dfrac{s}{a}$ （$a$ は定数）と書ける。

$ds^2=dx^2+dy^2$ より，

$\dfrac{ds}{dx}=\sqrt{1+\left(\dfrac{dy}{dx}\right)^2}=\dfrac{\sqrt{s^2+a^2}}{a}$

よって，$\displaystyle\int \dfrac{ds}{\sqrt{s^2+a^2}}=\displaystyle\int \dfrac{dx}{a}$

左辺の積分計算がめんどうなので詳細は省略するが，両辺積分して整理すると，

$s=a\sinh \dfrac{x}{a}=\dfrac{a(e^{\tfrac{x}{a}}-e^{-\tfrac{x}{a}})}{2}$

(境界条件は $x=0$ で $s=0$)

同様に，$\dfrac{ds}{dy}=\sqrt{1+\left(\dfrac{dx}{dy}\right)^2}=\dfrac{\sqrt{s^2+a^2}}{s}$

から，$\displaystyle\int \dfrac{sds}{\sqrt{s^2+a^2}}=\displaystyle\int dy$

の両辺を積分して $y=\sqrt{a^2+s^2}$

以上2式より $s$ を消去すれば懸垂線の式が得られる。

ひもに蓄えられた位置エネルギーは以下の式で表される：

$\displaystyle\int mgyds=\rho g\int y\sqrt{1+y^{\prime 2}}dx$

よって，$f=y\sqrt{1+y^{\prime 2}}$ とおいてオイラーラグランジュ方程式を用いるのが筋。

ただし，$f$ は $x$ を含まないので，ベルトラミの公式 $f-y^{\prime}\dfrac{\partial f}{\partial y^{\prime}}=C$ が使える：

$\dfrac{y}{\sqrt{1+y^{\prime 2}}}=C$

上式を整理する：

$\displaystyle\int \dfrac{Cdy}{\sqrt{y^2-C^2}}=\displaystyle\int dx$

よって，この式を積分することにより，懸垂線の一般式が得られる：

$y=C\cosh \left(\dfrac{x-A}{C}\right)$

特に，$x$ 軸対称な場合が重要で，そのときには積分定数は $A=0$ となり，目標の式を得る。