転置行列の意味・重要な7つの性質と証明
更新
行列に対して「行」と「列」を入れ替えた行列を転置行列と言う。
転置行列の意味・性質・その証明を整理しました。
転置行列について
転置行列について
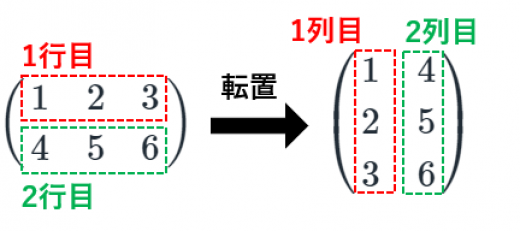
の転置行列は
- 転置を取ると1行目が1列目になり,2行目が2列目になります。
- このように, 行列に対してその転置行列は になります。
- 転置行列は「すべての に対して 成分と 成分を交換したもの」と言うこともできます。
- の転置行列を と書くことが多いです。
転置行列と内積
転置行列と内積
2本のベクトル の内積 は と表すことがあります。
,
とする(それぞれ2×1サイズの行列とみなせる)と, は内積 と一致する。
転置行列の性質
転置行列の性質
覚えておくべき転置行列の性質を整理しました。
任意の行列 に対して,
任意の正方行列 に対して,
- の固有値と の固有値は等しい
- のランクと のランクは等しい
積 が定義できるサイズのとき
が正則なとき,
7つともよく使います。以下では1から7まで順に証明していきます。
転置行列の性質の証明
「転置の転置はもとに戻る」という性質です。
「行と列を交換する」という操作を2回したらもとに戻るのでOK。
「トレースは転置しても変わらない」という性質です。
転置行列とトレースの定義からわかります。実際, のサイズを とすると
「行列式は転置しても変わらない」という性質です。一般的に書こうとするとかなりごちゃごちゃしたので の場合で説明します。一般の場合も全く同様に証明できます。
行列式の定義より,
を展開したときの項は 個あるが,例えば4次の置換
に対応する項として, が出てくる。
一方, を展開したときも同様に24項出てくるが, の逆置換:
に対応する項として, が出てくる。
ここで,ある置換とその逆置換の符号は等しいので, である。よって,上記の項は等しい。
他の項についても同様の議論が成り立つ。つまり, を展開したときの各項と を展開したときの各項の間には1対1対応があり,対応する項の値は等しいことが分かる。
以上により転置行列の行列式はもとの行列の行列式と同じであることが証明された。
- の固有値と の固有値は等しい
の固有値 は固有方程式 の解である。
これを変形すると,
ここで,性質3より行列式は転置しても変わらないので,
これは, の固有方程式なので, と の固有値は同じ。
- のランクと のランクは等しい
ランクが「1次独立な行ベクトルの最大本数」であり,かつ「1次独立な列ベクトルの最大本数」であること(→行列のランクの意味(8通りの同値な定義)の2と3) から以下のようにわかる:
のランク
=「 において1次独立な行ベクトルの最大本数」
=「 において1次独立な列ベクトルの最大本数」
= のランク
「積の転置は順番を交換して転置の積」という性質です。
成分計算するのみ(行列積の成分表示に慣れる練習になる。よくわからない人はサイズが小さい場合で確認することを推奨)。
の列数(= の行数)を とおきます。
の 成分は の 成分。つまり,
一方, の 成分は となり上式と一致する。
ちなみに,性質6を繰り返し使うと, のように数が増えても「積の転置は順番を交換して転置の積」が成立することがわかります。
-
「転置の逆行列は逆行列の転置」という性質です。
6において とおくと,
これは, が の逆行列であることを表している。
練習問題
練習問題
転置行列の性質を覚えているとサクサク計算できる例題です。
が正則である任意の行列 に対して とおくと, になることを確認せよ。
射影行列のイメージと楽しい公式で出てくる直交射影行列です。
転置行列の性質を使って確認します。
性質6より,上式は
性質1と性質7より,上式は
さらに性質1と性質6より,上式は
となり がわかった。
転置行列により定義される行列
転置行列により定義される行列
「転置」はいろいろな特殊な行列の定義に現れます。
- 対称行列 →対称行列の定義と性質~固有値と固有ベクトルの性質
- 直交行列 →直交行列の5つの定義と性質の証明
- 交代行列 →交代行列の定義と性質
- 射影行列 →射影行列のイメージと楽しい公式
性質1~7の証明がスラスラできれば,線形代数の基礎(行列式、トレース、固有値、ランク、逆行列)をしっかり理解できています。











