行列式の３つの定義・性質・意味

更新 2022/02/24

行列式とは，正方行列に対して決まる重要な量（スカラー）である。行列 $A$ の行列式を $\det A$ や $|A|$ と表す。例えば

$A=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}$

の行列式は， $a_{11}a_{22}-a_{12}a_{21}$ となる。

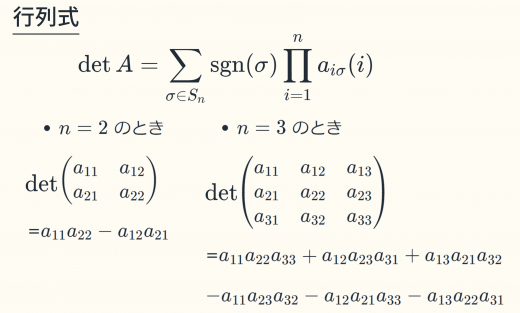
行列式の定義

この記事では，行列式の定義と性質について解説します。

行列式の定義

まずは，行列式の定義をきちんと解説します。

定義自体は抽象的で分かりにくいと思いますが， $2\times 2$ 行列， $3\times 3$ 行列の場合は簡単に計算できます。

行列式1

$A$ を $n \times n$ 行列として $ij$ 成分を $a_{ij}$ とする。このとき，行列式を $\begin{aligned} \det A &= \sum_{\sigma\in S_n}\mathrm{sgn} (\sigma) \prod_{i=1}^na_{i\sigma(i)}\\ &= \sum_{\sigma\in S_n}\mathrm{sgn} (\sigma) a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{n\sigma(n)} \end{aligned}$ と定める。

$S_n$ は $n$ 次置換群です。つまり $\sigma$ は $1$ から $n$ の置換（順列）を表します。 $\displaystyle\sum_{\sigma\in S_n}$ というのは，「 $n$ 次の全ての置換に関して和を取る」ことを表しています。→ 対称群と交代群の基本的な性質
$\mathrm{sgn} (\sigma)$ は置換の符号を表しています。奇置換なら $-1$ ，偶置換なら $+1$ です。置換については→置換の基礎（互換・偶置換・奇置換・符号の意味）を参照して下さい。

サイズ2，サイズ3の場合の行列式の公式

置換による行列式の定義は分かりにくいので，小さいサイズの行列を例に確認してみます。

記法

置換 $\sigma$ は $\begin{bmatrix} 1 & 2 & \cdots & n\\ \sigma (1) & \sigma (2) & \cdots & \sigma (n) \end{bmatrix}$ というように，上の段に $1,2, \cdots , n$ を，下の段に $1,2, \cdots , n$ の移動先を書くことで表現します。

$2 \times 2$ 行列の行列式

公式

2×2行列の行列式

$A=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}$ の行列式は， $a_{11}a_{22}-a_{12}a_{21}$ である。

証明

$S_2$ の元（ $1,2$ の置換）は $\sigma_1 = \begin{bmatrix} 1 & 2\\ 1 & 2 \end{bmatrix}, \sigma_2 = \begin{bmatrix} 1 & 2\\ 2 & 1 \end{bmatrix}$ の2つなのでそれに従って行列式には二つの項が出てきます。

$\mathrm{sgn} (\sigma_1) = 1, \mathrm{sgn} (\sigma_2) = -1$ であるため， $\begin{aligned} &\det \begin{pmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{pmatrix}\\ &= \mathrm{sgn} (\sigma_1) a_{1\sigma_1(1)} a_{2 \sigma_1 (2)} + \mathrm{sgn} (\sigma_2) a_{1\sigma_2(1)} a_{2 \sigma_2 (2)}\\ &= a_{11} a_{22} - a_{12} a_{21} \end{aligned}$ となります。

$3 \times 3$ 行列の行列式

公式

2×2行列の行列式

$A=\begin{pmatrix} a_{11} & a_{12} &a_{13}\\ a_{21} & a_{22} &a_{23}\\ a_{31} & a_{32} &a_{33}\\ \end{pmatrix}$ の行列式は，

$\begin{aligned} &a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\\ &-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31} \end{aligned}$

である。

証明

$1,2,3$ の置換（並べ替え）は6つなので，それに従って行列式には6つの項が出てきます。例えば三項目は $\begin{bmatrix} 1&2&3\\ 3&1&2 \end{bmatrix}$ という置換に対応しています。置換の符号によってそれぞれの項がマイナスかプラスかが決まります。

同様に $4$ 次の行列の行列式には項数が $4!=24$ 個出てくるのでもはや書き下すのは厳しいです。 $n$ 次の行列式には $n!$ 個の項が登場します。

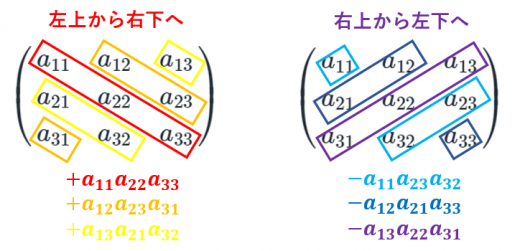
サラスの公式

$3 \times 3$ 行列の行列式には，サラスの公式という式があります。

サラスの公式

3×3の行列の行列式は

「左上から右下にかけて足す」 $-$ 「右上から左下にかけて足す」

という方法で計算できる。サラスの公式

→ サラスの公式と使い方

行列式の性質

上記のように行列式を定義すると，以下の3つの性質が成立します。

行列式2

性質1：単位行列 $I$ に関して $\det I=1$

性質2（交代性）： $i$ 列と $j$ 列を交換すると行列式は $-1$ 倍される

性質3（多重線形性）：一つの列以外固定して一つの列の関数と見たときに線形性が成立する。

逆に上記の3つの性質を満たす関数は行列式のみです。つまり行列式とは上記の3つの性質を満たすものと定義することもできます。

これが行列式の二つ目の定義です。こちらを定義とみなせば，さきほどの定義1は行列式の性質として導かれます。

行列式の意味（平行六面体の体積）

行列式の非常に美しい性質（図形的な意味）です。
行列
AAA
 を縦ベクトルを
nnn
 本並べたものと見ます：
A=(a1undefined, a2undefined,⋯ ,anundefined)A=(\overrightarrow{a_1},\:\overrightarrow{a_2},\cdots, \overrightarrow{a_n})A=(a1​​,a2​​,⋯,an​​)
  すると，
aiundefined\overrightarrow{a_i}ai​​ たちが張る平行六面体の体積は行列式（の絶対値）と一致します。
n=2n=2n=2
 の場合，二本のベクトルが張る平行四辺形の面積の半分が三角形の面積。
n=3n=3n=3
 の場合，三本のベクトルが張る平行六面体の体積の
16\dfrac{1}{6}61​
 倍が四面体の体積です。
→サラスの公式
n≥4n\geq 4n≥4
 の場合，そもそも
nnn
 次元空間中の立体の体積ってなんだ？って話になってしまいますが詳細は割愛します。
なお，この性質を使って行列式を定義することもできます。すなわち，列ベクトルたちが張る平行六面体の（符号付き）体積が行列式であると定義します。これが行列式の3つ目の定義（「行列式3」とする）です。

3つの定義

「行列式1（置換）」「行列式2（3つの性質）」「行列式3（体積）」の定義はいずれも同値です。

1を認めれば2は簡単に確かめられます。
2を認めたときに1を導くのはけっこう大変ですが計算でできます。
符号付き体積が3つの性質を満たすことも確認できるので2と3は同値です。

よってどれを定義と思ってもOKです。一つの定義に固執することなく行列式は行列に関する重要な量でいろいろな見方があると覚えておきましょう。

私は置換による定義が好きです。

Tag:数検1級の範囲と必要な公式まとめ

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！

行列式の３つの定義・性質・意味

行列式の定義

サイズ2，サイズ3の場合の行列式の公式

2×22 \times 22×2 行列の行列式

公式

3×33 \times 33×3 行列の行列式

公式

サラスの公式

行列式の性質

行列式の意味（平行六面体の体積）

3つの定義

$2 \times 2$ 行列の行列式

$3 \times 3$ 行列の行列式