冒頭の定理を証明します。主張を3つにわけてそれぞれ証明します:
- そもそも AA⊤ に逆行列 (AA⊤)−1 が存在すること。
- x∗=A⊤(AA⊤)−1b が Ax=b の解であること。
- Ax=b なる任意の x に対して ∥x∥2≧∥x∗∥2 であること。
1の証明
AA⊤ が正則であることを証明する。具体的には,行列が正則であることの意味と5つの条件の条件4「AA⊤x=0 なら x=0」を証明する。
AA⊤x=0 なら x⊤AA⊤x=0,つまり (A⊤x)⊤(A⊤x)=0
∥A⊤x∥22=0
長さが 0 であるベクトルは 0 のみなので
A⊤x=0
ここで,定理の仮定より A の行ベクトルが線形独立なので,A⊤ の列ベクトルが線形独立。つまり x=0 がわかる。
2の証明
Ax∗=(AA⊤)(AA⊤)−1b=b
3の証明
∥x∥22=∥x−x∗+x∗∥22=∥x−x∗∥22+∥x∗∥22+2(x−x∗)⊤x∗
ここで「Ax=b のとき第三項が 0」なら ∥x∥2≧∥x∗∥2 がわかる。以下では「Ax=b のとき第三項が 0」を示す:
(x−x∗)⊤x∗=(x−x∗)⊤A⊤(AA⊤)−1b=(Ax−Ax∗)⊤(AA⊤)−1b=(b−b)(AA⊤)−1b=0
参考文献:Least-norm solutions of undetermined
equations
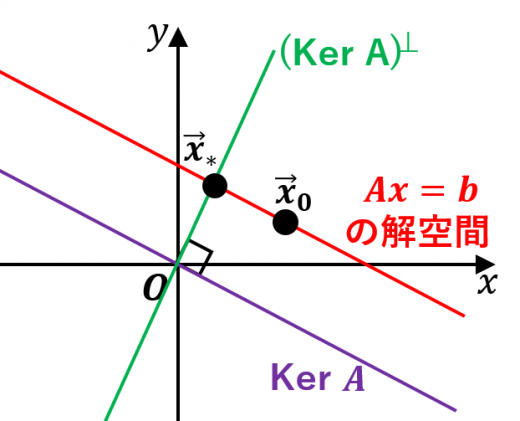 図のように理解できます。図の説明:
図のように理解できます。図の説明:










