余因子と余因子行列

更新 2023/08/28

線形代数の基礎である余因子と余因子行列についてわかりやすく説明します。

余因子の意味と例

余因子とは

正方行列に対して

「 $i$ 行目と $j$ 列目を除いた行列」の行列式に $(-1)^{i+j}$ をかけたもの

を $(i,j)$ 余因子と言う。

例1

例えば， $3\times 3$ 行列 $A=\begin{pmatrix}1&2&3\\4&5&6\\-2&0&1\end{pmatrix}$ に対して $(2,1)$ 余因子を計算してみよう。

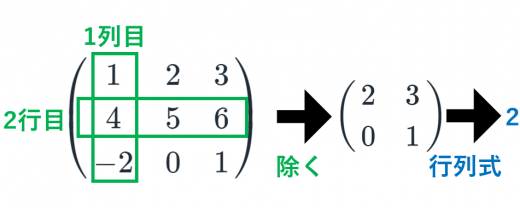
余因子の例

$A$ から， $2$ 行目と $1$ 列目を除いた行列 $\begin{pmatrix}2&3\\0&1\end{pmatrix}$ の行列式 $2\times 1-3\times 0=2$ に $(-1)^{2+1}=-1$ をかけた $-2$ が答えである。

以下， $(i,j)$ 余因子のことを $\Delta_{ij}$ と書くことにします。

余因子行列の意味と例

余因子行列とは

正方行列 $A$ に対して，

$(i,j)$ 余因子 $\Delta_{ij}$ を $ij$ 成分に持つ行列を転置したもの

を余因子行列と言う。

例2

例1の行列 $A=\begin{pmatrix}1&2&3\\4&5&6\\-2&0&1\end{pmatrix}$ の余因子行列を計算しよう。

$(2,1)$ 余因子は $-2$ であった。他の8つの余因子も計算して転置を取ると $\begin{pmatrix}5&-2&-3\\-16&7&6\\10&-4&-3\end{pmatrix}$ となる。これが $A$ の余因子行列である。余因子行列の例

参考：転置行列の意味・重要な7つの性質と証明

逆行列との関係

以下， $A$ の余因子行列を $\tilde{A}$ と書きます。

定理1

$A$ が正則なら， $A\:\dfrac{\tilde{A}}{\det A}=I$

つまり， $A$ の逆行列は，余因子行列 $\tilde{A}$ を定数倍（ $\dfrac{1}{\det A}$ 倍）したもの）

著しい性質です。余因子行列を計算することで，逆行列が計算できます！余因子の定義で「なぜ $(-1)^{i+j}$ をつけるの？」と思ったり，余因子行列の定義で「なぜ転置するの？」と思った人もいるでしょうが，これらのおかげで定理1が成り立ちます！

以下，定理1の証明が目標です。そのために「余因子展開」を紹介します。

余因子展開

$A$ を $n\times n$ 行列とします。

定理2（余因子展開）

任意の $i$ に対して， $\displaystyle\sum_{j=1}^n a_{ij}\Delta_{ij}=\det A$

$A\tilde{A}$ の $ii$ 成分が $\det A$ であることを表しています。つまり，定理1の対角成分に対応します。
行列式を分解しています。この式を余因子展開と言います。

例

一般の場合の定理2の証明は少し込み入っているので， $n=3$ ， $i=2$ の場合の例を見てみる。つまり， $a_{21}\Delta_{21}+a_{22}\Delta_{22}+a_{23}\Delta_{23}=\det A$ を確認する。

$\det A\\ =a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\\ -a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31}$

であるが， $a_{21},a_{22},a_{23}$ のどれが登場するかで3グループにわけると，

まず， $a_{21}$ が登場する部分は $a_{21}(a_{13}a_{32}-a_{12}a_{33})$ となる。これを変形すると $a_{21}\times(-1)^{2+1}(a_{12}a_{33}-a_{13}a_{32})=a_{21}\Delta_{21}$ となる。
同様に $a_{22}$ が登場する部分は $a_{22}\Delta_{22}$ になる。
同様に $a_{23}$ が登場する部分は $a_{23}\Delta_{23}$ になる。

定理2の証明の概要

行列式の置換による定義 $\det A=\displaystyle\sum_{\sigma\in S_n}\mathrm{sgn}(\sigma)\prod_{k=1}^na_{k\sigma(k)}$ を思い出そう。この右辺の和の中で $\sigma(i)=j$ の値で $n$ グループに分けて足し上げると， $\det A=\sum_{j=1}^na_{ij}\displaystyle\sum_{\sigma(i)=j}\mathrm{sgn}(\sigma)\prod_{k\neq i} a_{k\sigma(k)}$ 実は，上式のシグマ以降は余因子と一致する： $\displaystyle\sum_{\sigma(i)=j}\mathrm{sgn}(\sigma)\prod_{k\neq i} a_{k\sigma(k)}=\Delta_{ij}$ （ $A$ の $i$ 行目と $j$ 列目を除いた行列の行列式を考えると，符号× $\displaystyle\prod_{k\neq i} a_{k\sigma(k)}$ が出てくる。符号部分が難しいが，少し考えると $\mathrm{sgn}(\sigma)\times(-1)^{i+j-2}$ と一致することがわかる）

定理2から定理1を証明

定理1における対角成分は定理2そのもの。

あとは，非対角の $ij$ 成分 $i\neq j$ を示す。示したい式は， $\displaystyle\sum_{k=1}^na_{ik}\Delta_{jk}=0$ である。実は，これは定理2からわかる。

「 $A$ の $j$ 行目を $i$ 行目で置き換えた行列」を $B$ とする。 $B$ に定理2を適用すると， $\displaystyle\sum_{k=1}^nb_{jk}\Delta_{jk}=\det B$ となるが， $b_{jk}=a_{ik}$ であることと，（2つの行が同じ行列の行列式は $0$ より） $\det B=0$ であることから緑色の式がわかる。

逆行列の計算

余因子行列を計算すれば，それを行列式で割ることで逆行列を計算できます。

しかし，余因子行列の計算はとてもめんどうです。例えば $4\times 4$ 行列の余因子行列を計算するには， $3\times 3$ 行列の行列式を $16$ 回も計算する必要があります。

実は，逆行列を計算するだけなら掃き出し法の方が簡単です。→逆行列の定義・逆行列を求める２通りの方法と例題

余因子行列は理論的におもしろいですが，逆行列の手計算には向いていません。

$4\times 4$ 行列の余因子行列を手計算してみてください。二度とやりたくないと思うでしょう。

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！