ボルツァーノ=ワイエルシュトラスの定理
更新
実数列 が有界であるとき, は収束する部分列を持つ。
ボルツァーノ=ワイエルシュトラスの定理は,解析学・集合位相空間論において重要な定理です。
2通りの証明を紹介します。
証明1:単調収束定理を用いる証明
証明1:単調収束定理を用いる証明
1つめの証明は単調収束定理を用いた証明です。単調収束定理自体も非常に有用です。
単調収束定理
有界な数列 は広義単調増加,もしくは広義単調減少な数列とする。このとき は収束する。
証明は 有界とは何か~上界・上限と下界・下限 で紹介した上限の性質
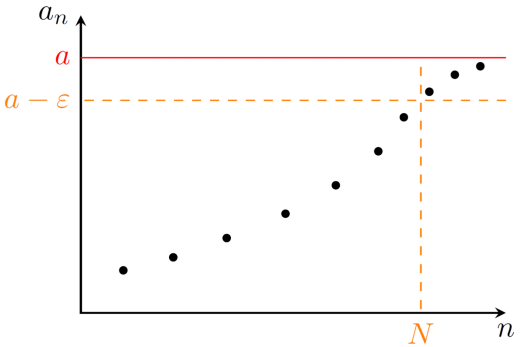
が の上限であることは,次の2つを満たすことと同値:
- 任意の に対して
- を任意に取ったとき,ある があって となる。
を活用します。以下では「広義単調増加」のことを単に「単調増加」と言います。
単調増加するときのみを考える。
とおく。 を示す。
は上限であるため,任意の に対して,ある が存在して となる。
加えて より である。
は単調増加であるため, において となる。つまり, となるため, が示された。
※単調収束定理の応用例はこの記事の末尾にあります。
証明
単調収束定理を使って,ボルツァーノ=ワイエルシュトラスの定理(有界なら収束部分列を持つ)を証明します。
数列 が単調な部分列を持つことを示せば,単調収束定理からその部分列が収束することがわかります。
単調な部分列の取り方は非常におもしろいです。
自然数 に対して,性質 を次のように定める。
: なる任意の自然数に対して
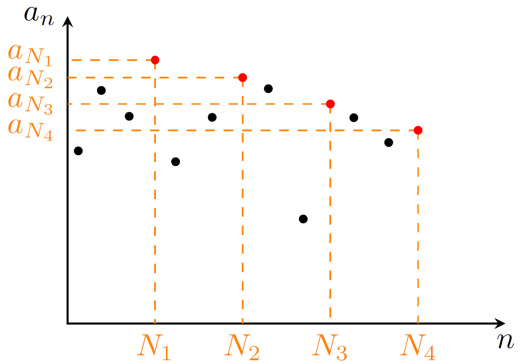
1. を満たす自然数が無限個存在するとき
を満たす自然数 に対して,同じく を満たす自然数 を取ることができる。 から である。
に対しても同様に を取ることで とできる。
こうして帰納的に を満たす自然数 を無限に取ると,部分列 は単調に減少する部分列である。
2. を満たす自然数が有限個のとき
を満たす最大の自然数を とする。
を取ると は を満たさないため,ある があって である。 に対しても同様に を取ることで とできる。
以下帰納的に を取ることで単調に増加する部分列 を得る。

仮定から は有界であるため,その部分列も有界である。こうして単調収束定理から 1,2で得た部分列が収束値を持つことが従い,証明が完了する。
証明2:区間縮小法を使う証明
証明2:区間縮小法を使う証明
もう1つの証明は区間縮小法と呼ばれる非常に美しい方法です。
その名の通り,数列の取りうる区間を縮めて,収束値を与える方法です。
は有界であるため,上限と下限が存在する。それぞれ とおく。 とおく。
とする。 は2つの区間 に分かれる。このうち少なくとも一方の区間は の元を無限個含む。そのような区間を とおき,端点を とおく。
同様にして帰納的に を定める。
 すると,
より
よって
となる。この値を とおく。
すると,
より
よって
となる。この値を とおく。
さて, の部分列 を から順に となるように(そして が単調増加になるように)取る。
このとき であるので,はさみうちの原理から となり,収束部分列を構成できた。
展望
展望
より一般の集合で「有界性」を考えるとき,このボルツァーノ=ワイエルシュトラスの定理が1つの道標になります。
定理の主張に現れた 任意の数列が収束する部分列を持つ という性質を満たした集合を 点列コンパクト集合 といいます。
つまり,ボルツァーノ=ワイエルシュトラスの定理は 実数の有界な部分集合は点列コンパクトである と言い換えられます。
これを「逆さ」に見ることで,一般の集合の有界性をコンパクト性から考えることができるようになります。コンパクト性は非常に有用で,例えば リー群論 において,コンパクトリー群 は非常に扱いやすいクラスとなります。
補足:単調収束定理の応用例
補足:単調収束定理の応用例
例題
数列 を , により定める。
このとき を求めよ。
この問題を単調収束定理によって解いてみてみましょう。
まず が有界かつ単調増加であることを示し,上限を計算することで極限値を求める。
とおく。
より は単調増加な関数である。
1. 単調増加になる条件
と置く。
を解くと である。
であるため, で は単調減少である。
よって において となり を得る。よって のとき となる。
2. であること
帰納法により を示す。
のときは条件より従う。
のとき成立を仮定する。
仮定より である。 は単調増加関数であるため である。, より である。以上より示された。
以上より は有界かつ単調増加であることがわかる。こうして単調収束定理から は収束値を持つ。
3. の上限の計算
単調収束定理の証明から,収束値は の上限である。これが であることを確認する。
上限 が より小さいと仮定する。
上限の性質から, を任意に取ったとき,ある があって となる。
今 と選ぶと であるため であり, が上限であることに反する。よって である。
こうして を得る。
ボルツァーノ=ワイエルシュトラスの定理の応用例として,最大値・最小値の定理 の証明があります。











