ローラン展開の意味・計算方法・特異点の分類
更新
で正則(微分可能)な複素関数 は,以下のようにべき級数展開できる。 ただし,各係数 は で計算できる ( は を満たす実数ならなんでもよい)。
これをローラン展開(Laurent展開・ローラン級数展開)といいます。右辺の級数をローラン級数といいます。
この記事ではローラン展開について詳しく紹介します。
正則関数のテイラー展開
正則関数のテイラー展開
- ローラン展開: は のまわりで関数 をべき級数に展開しています。
- テイラー展開と似ていますね! テイラー展開は から までの和ですが,ローラン展開ではマイナスの項があります。
- 実は,ローラン展開はテイラー展開の拡張です。というわけで,まずは複素関数のテイラー展開について再確認しましょう。
- ,
という記号を使います。 - 「正則」というのは,一階微分できるという意味です。ただし,複素関数では「一階微分可能なら何回でも微分可能」という著しい性質があります(→コーシーの積分公式とその応用のグルサの定理参照)。
- ここから少しむずかしいです。以下の「ローラン展開」の節まで読み飛ばしても構いません。
閉円盤 で正則な関数 を考える。コーシーの積分公式より,円盤内部の点 について
ただし, は円盤 の周を表す。ここで と展開できるので,
ただし,最後の等号は積分と無限和を交換した(→補足)。つまり, とおくと という級数展開が得られる。さらに,グルサの定理から
補足:無限和(級数)が一様収束するので積分と無限和を交換できます。実際,この級数が で一様収束することを確認しましょう。 とおくと,
-
として を で展開すると
-
を で展開すると
ローラン展開
ローラン展開
なぜローラン展開を考えるのか
正則ならテイラー展開すればよいのですが,正則でない関数もべき級数展開したいです! そこでローラン展開です。正則でなくてもその点のまわりで正則ならローラン展開できるのです。
まずは「その点のまわりで正則なら」の意味を詳しく説明します。
孤立特異点
関数 に対して,「 で正則ではないが, で正則となる」ような正の実数 が存在するとき, を の孤立特異点という。
孤立特異点の例を見てみましょう。
-
は で定義されていません。一方 では正則です。よって は の孤立特異点となります。
-
とすると は で孤立特異点を持ちます。
上の例では 全体で特異点が有限個しかないパターンでしたが,そうでない例もあります。
- は で正則ではありません。ですが, とすれば, で正則です。つまり, は の孤立特異点です。
孤立特異点の近傍で級数展開
孤立特異点の近傍でもべき級数展開したいのですが,テイラー展開はできません。なぜなら,特異点では微分ができないため,以下のテイラー展開の式の2が計算できないからです:
一方,グルサの定理より微分可能な場合は
が成立します。そこで,微分できない場合も,係数を
2’.
で定めればべき級数展開できるのではないか?と考えてみます。2’なら が微分できなくても計算できますね。実は,この2’に基づくと,
1’.
が成立します!( が からではなく から動く)
1’と2’でうまくいく証明は記事末でしっかり説明しますが,とりあえずローラン展開はテイラー展開を孤立特異点でも使えるように拡張したものと理解しておきましょう。実際, で正則ならローラン展開とテイラー展開は一致します(なぜなら, のとき の表式の被積分関数は正則になり,コーシーの積分定理より になって負の部分が消えるから)。
ローラン展開の計算方法
ローラン展開では積分によって係数 を計算できます。しかし,必ず積分しないといけないわけではありません。ローラン展開は一意に定まる(以下の補題)ので,何かしらの方法で頑張って
を満たす を見つけてくればよいわけです。あくまでも積分の計算はローラン展開を求める1つの手段です。むしろ,積分を忠実に計算することは少ない気がします。
を 近傍でローラン展開してみる。
なお,計算の過程で のローラン展開を使った。
ローラン展開は一意に定まる。つまり,正則関数 に広義一様収束する級数展開が2種類あるなら両者の係数は一致する。
と という2種類の級数展開ができたとする。
任意に をとる。級数は一様収束することから
と変形できる。ここで を思い出すと が得られる。同様の計算を に当てはめると が得られる。こうして となり展開の一意性が示された。
例題
ローラン展開の問題を解いてみましょう。
次の関数をローラン展開しなさい。
- ( の周りで)
- ( の周りで)
- ( の周りで)
-
のマクローリン展開を用いる。 (ただし, も特異点なので,この式の成立範囲は である)
-
のマクローリン展開を用いる。
-
のマクローリン展開を用いる。
特異点の分類
特異点の分類
- ローラン展開とテイラー展開の違いとして「負の部分の有無」があります。
- 負の部分を主要部もしくは特異部といいます。
- 孤立特異点はそのローラン展開の主要部により3つのパターンに分解できます。
可除特異点
のようにローラン展開に主要部が現れない特異点を可除特異点(除去可能特異点・見かけ上の特異点)といいます。**特異点が可除特異点であるとき,複素関数 を延長すれば( を適切に定めれば)特異点を含む領域で正則になります。**このため,可除特異点は,特異点とカウントしないことが多いです。
なお,可除特異点であるかどうかローラン展開をせずに判定する方法があります。詳しくは,リーマンの可除特異点定理を読んでみてください。
極
のように主要部がどこかで終わる場合,極といいます。 次まで主要部があるとき, 位の極といいます。
例えば では が 位の極となります。
真性特異点
のように上記のどちらでもない場合,真性特異点といいます。
真性特異点に関連する定理には非常に興味深いものがあります。ここでは簡単に主張を紹介するにとどめます。
は で正則であり, を真性特異点に持つとする。
このとき,ある があって,任意の に対して,ある であって を満たすものが取れる。
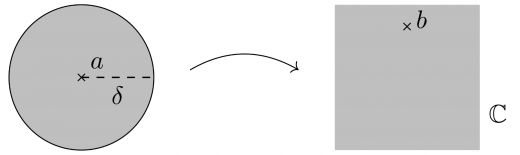
ピカールの大定理は,「真性特異点近傍の像が,複素数全体をほとんど覆ってしまうこと」を意味します。証明も興味深いため是非調べてみてください。
ローラン展開の証明
ローラン展開の証明
それではローラン展開の証明です。まずは,より強い形でローラン展開の主張を書き下します。
とする。複素関数 が で正則とする。
このとき, を満たす任意の について,
ただし,各係数は なる任意の を選んで で計算できる。
冒頭の主張は上記で とした場合です。
証明は,正則関数のテイラー展開とほぼ同じですが,特異点を避けるようにコーシーの積分公式を適用することになります。
なる を1つ選んで固定する。 を満たす を取ってくる。
領域 にコーシーの積分公式を適用する(→補足)と となる。

一項目について式を変形する。 この無限級数は で一様収束するため,一項目は積分と極限を交換できる。
二項目についても同様に変形を行う。 この無限級数は で一様収束するため,二項目でも積分と極限を入れかえることができる。
以上より と展開できた。
補足:領域 はドーナツ型で穴があります。コーシーの積分公式の記事中でも言及しましたが,コーシーの積分公式は,単純曲線に囲われた領域に当てはまるもので,穴があっても適用できます。
留数定理に向けて
留数定理に向けて
複素関数を積分するとき,元の関数の表示ではなくローラン展開したものを積分することを考えましょう(一様収束することから,項別積分できます)。ローラン展開の一意性を確認したときに登場した公式 を思い出すと, 次の項,すなわち だけが積分結果に関与しそうです。このことをより一般に述べた定理が留数定理です。
次回は留数定理を紹介します。留数定理を用いると様々な実積分が複素関数論の力で計算できるようになります。お楽しみに!
ローラン展開の計算は楽しいですね。











