コーシーの積分定理と積分経路の変形

• 領域とは，連結な開集合のことを指します。連結であるとは，飛び地がない集合のことを意味します。

• この記事では，単連結な領域を考えます。つながっていて穴がない領域です。

• 正則関数とは，考えている領域内で（複素）微分可能な関数のことです。詳しくは，コーシーリーマンの関係式と微分可能性・正則関数 を確認してください。

• 単純閉曲線とは，「曲線の始点と終点が一致」して「始点と終点以外で自分と交わらない」ような曲線です。この記事では，区分的になめらかな曲線（なめらかな曲線の合併）を考えます。

• 積分経路が閉曲線であるとき，$\displaystyle \oint$ という記号を用います。このように，閉曲線に沿った（複素）線積分を周回積分ということがあります。

特殊な場合について，証明を紹介します。

グリーンの定理を用いた証明

コーシーの積分定理の有名な証明としてグリーンの定理を用いたものがあります。なお，この証明では正則関数 $f$ の導関数が連続であることを仮定しています。

原始関数の存在を仮定した証明

複素積分の導入 で登場した以下の定理を使います。

この定理で $c(a) = c(b)$ 場合を考えると，コーシーの積分定理が得られます。

なお領域 $D$ 内で正則な関数に原始関数が存在することの証明は可能ですが長いので，省略します。興味がある人は複素解析の本を読んでみてください。

積分路の変形

コーシーの積分定理を用いると，領域 $D$ 内で自由に積分経路を変形できます。

つまり，下図のように2つの向きの付いた閉曲線 $C_1$，$C_2$ を考えたとき

$$\oint_{C_1} f(z) \; dz = \oint_{C_2} f(z) \; dz$$

となることを示します。ただし，$f(z)$ は $D$ 内で正則な任意の関数です。

$C_1$ と $C_2$ の間に「切れ目」として $L$ を入れることにします。

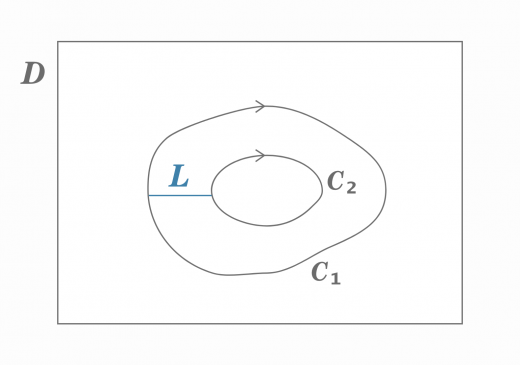
わかりやすく見るために，下図のように曲線を分けた図を考えます。

$C_1$ と $C_2$ と $L$ により，閉曲線ができていることがわかりますね。この新たな閉曲線を $C'$ としましょう。$C'$ に新たな向きを付けましょう。

上図のように向きを付け積分を考えるとコーシーの積分定理により

$$\oint_{C'} f(z) \; dz =0$$ となります。ここで $C' = C_1 + L - C_2 - L$ という経路で分解できることに注意すると， $$\begin{aligned} &\oint_{C'} f(z) \; dz\\ &= \oint_{C_1 + L - C_2 - L} f(z) \; dz\\ &= \oint_{C_1} f(z) \; dz + \oint_{L} f(z) \; dz + \oint_{- C_2} f(z) \; dz +\oint_{- L} f(z) \; dz\\ &= \oint_{C_1} f(z) \; dz + \oint_{L} f(z) \; dz - \oint_{C_2} f(z) \; dz - \oint_{L} f(z) \; dz\\ &= \oint_{C_1} f(z) \; dz - \oint_{C_2} f(z) \; dz \end{aligned}$$ と変形されます。すなわち $$\oint_{C_1} f(z) \; dz - \oint_{C_2} f(z) \; dz = \oint_{C'} f(z) \; dz =0$$ となり $$\oint_{C_1} f(z) \; dz = \oint_{C_2} f(z) \; dz$$ が得られます。

被積分関数の正則性

先ほどは $f(z)$ が $D$ 内で正則であるとしましたが，上の議論より 「$C_1$ と $C_2$ で囲まれた部分の周と内部を含むある領域」で正則であれば十分**です。

具体例

複素積分の導入で登場した例題を思い出しましょう。

どちらの積分経路でも $f(z)$ の積分は $i$ となりました。

$f(z) = x + iy$ は $\mathbb{C}$ 上で正則です。そのため $C$，$C_1$，$C_2$ に囲まれた領域上でももちろん正則になります。そのため積分経路を変更しても積分値が同じだったのです。

この場合は2つの経路で積分値が異なります。実際， $$\int_{C_{1}} \dfrac{dz}{1+z} = i\pi\\ \int_{C_{2}} \dfrac{dz}{1+z} = -i\pi$$ でした。

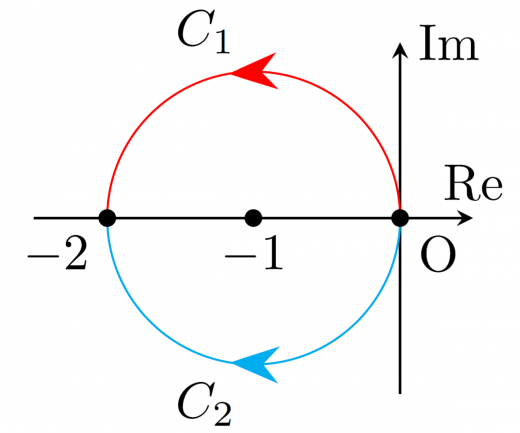
$C_1$ と $C_2$ によって囲まれた領域を確認しましょう。領域内に $(-1)$ という点があります。被積分関数 $f(z) = \dfrac{1}{1+z}$ は $(-1)$ で正則ではありません。そのため積分経路によって値が変わったのです。

$\quad$

さて前回の振り返りはここまでにして，積分経路の変形を活用する問題に挑戦してみましょう。

このままの形では積分が難しいため，部分分数分解をすることで扱いやすい形にします。

$$\dfrac{2z}{z^2-1} = \dfrac{1}{z-1} + \dfrac{1}{z+1}$$ であるため $$\oint_C \dfrac{2z}{z^2-1} dz = \oint_C \dfrac{1}{z-1} dz + \oint_C \dfrac{1}{z+1} dz$$ となります。

ここで $C_1 : (x-1)^2 + y^2 =\dfrac{1}{4}$，$C_2 : (x+1)^2 + y^2 = \dfrac{1}{4}$ という2曲線を考えます（向きは反時計回りにつけます）。

$\dfrac{1}{z-1}$ は $C$ と $C_1$ の間の領域で正則であるため，積分経路の変形ができ $$\oint_C \dfrac{1}{z-1} dz = \oint_{C_1} \dfrac{1}{z-1} dz$$ です。$C_1$ は $c_1 (t) = \dfrac{1}{2} e^{it} +1 \; (0 \leqq t \leqq 2\pi)$ で定義されるため， $$\begin{aligned} \oint_{C_1} \dfrac{1}{z-1} dz &= \int_0^{2\pi} \dfrac{c_1' (t)}{c_1 (t) - 1} dt\\ &= \int_0^{2\pi} \dfrac{1}{2} ie^{it} \dfrac{2}{e^{it}} dt\\ &= \int_0^{2\pi} i \; dt = 2\pi i \end{aligned}$$ となります。

$\dfrac{1}{z+1}$ においても同様に $C$ から $C_2$ に積分経路を変形できます。$C_2$ は $c_2 (t) = \dfrac{1}{2} e^{it} -1 \; (0 \leqq t \leqq 2\pi)$ で定義され， $$\begin{aligned} \oint_{C} \dfrac{1}{z+1} dz &= \oint_{C_2} \dfrac{1}{z+1} dz\\ &= \int_0^{2\pi} \dfrac{c_2' (t)}{c_2 (t) +1} dt\\ &= \int_0^{2\pi} \dfrac{1}{2} ie^{it} \dfrac{2}{e^{it}} dt\\ &= \int_0^{2\pi} i \; dt = 2\pi i \end{aligned}$$ となります。こうして $$\oint_C \dfrac{2z}{z^2-1} dz = 2\pi i + 2\pi i = 4\pi i$$ が得られます。

次回予告

$\dfrac{1}{z-1}$ の積分をもう少し注意してみましょう。$C_1$ の半径が $2$ だった場合，どうなるでしょうか。

このとき $C_1$ は $c_1 (t) = 2 e^{it} +1 \; (0 \leqq t \leqq 2\pi)$ で定義されるため， $$\begin{aligned} \oint_{C_1} \dfrac{1}{z-1} dz &= \int_0^{2\pi} \dfrac{c_1' (t)}{c_1 (t) - 1} dt\\ &= \int_0^{2\pi} 2 ie^{it} \dfrac{1}{2 e^{it}} dt\\ &= \int_0^{2\pi} i \; dt = 2\pi i \end{aligned}$$ となります。

積分の値が一致しました。半径が $\dfrac{1}{2}$ の円と半径が $2$ の円の間で $\dfrac{1}{z-1}$ は正則ですから，実のところ積分経路の変換を考えれば計算するまでもありません。

さて，$z = \alpha$ を囲う単純閉曲線 $C$ で $\dfrac{1}{z-\alpha}$ を積分することを考えましょう。先ほどの計算から積分値は $2\pi i$ になることはすぐにわかるでしょう。これは コーシーの積分公式（積分表示） の特殊ケースです。というわけで次回はコーシーの積分公式及びそれに付随する定理を解説します。→コーシーの積分公式とその応用～グルサの定理・モレラの定理