複素積分の導入~複素線積分とその性質
更新
複素積分には非常に豊かな世界が広がっており,留数定理やコーシーの積分公式などの多種多様な定理・公式があります。
複素数の世界で積分をし,それを実数の世界に「もちこむ」ことで興味深い積分が計算できることもあります。例えばフレネル積分は の積分で,実の範囲だけでは計算ができません。
この記事では複素積分の導入を行います。例題も用意しています。複素解析への第一歩を踏み出しましょう。
複素積分では何が問題となるのか
複素積分では何が問題となるのか
これまで触れてきた積分は積分区間が実数でした。この「実数」を「複素数」に拡張するとどうなるのでしょうか。
経路
関数 を から で(実)積分することを考えましょう。 を から に動かして足し合わせるイメージです。一方, から へ複素数で積分するときのことを考えてみましょう。 をどのように動かすことになるのでしょうか。
から へ直線に沿うように? から を経由して に行く?
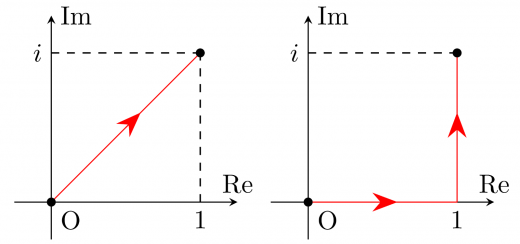
このように,「複素数で積分する」ときは,いろいろな動かし方が考えられます。複素数平面とあるように,複素数の世界が二次元的に広がっているためこのような問題が発生します。
そこで,線積分というものを考えます。こうした文脈から,複素積分には「複素線積分」という表現がしばしば用いられます。
複素積分は経路によって積分値が異なることがあります。そのため,経路を意識する必要があります。
準備:なめらかな曲線
準備:なめらかな曲線
複素積分では「経路(曲線)」が重要です。そこで,パラメタが付けられた曲線を考えます。
曲線 はパラメタ によって で定められるとします。複素数平面上の曲線を考えるため, の実部,虚部をそれぞれ , で表します。
なめらかな曲線
なめらかな曲線とは,とがったところがないような曲線のことです。より厳密な定義は以下です。
で定められた曲線 がなめらかであるとは,以下の2つを満たすことを指す。
- が 級である。すなわち が微分可能で,これらの導関数は連続である。
- の各点で接線が確定する。すなわち任意の で である。
例を2つ見てみましょう。
- 下図の は原点で「尖って」います。実際, で となっています。そのため, を で定義したとき,これはなめらかではなりません。一方で で定義すると,なめらかな曲線になります。
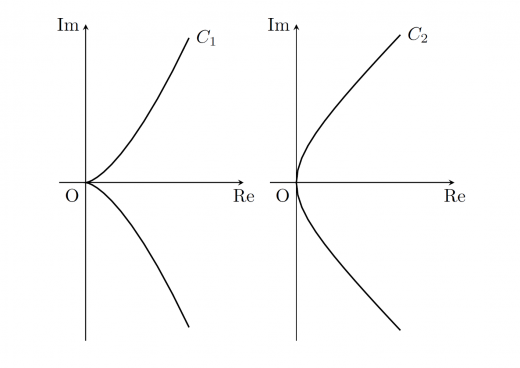
- は,任意の区間でなめらかな曲線となります。
曲線の逆・結合
曲線の逆と結合を定義します。文字でわかりにくい場合は,図を見てイメージしてください。
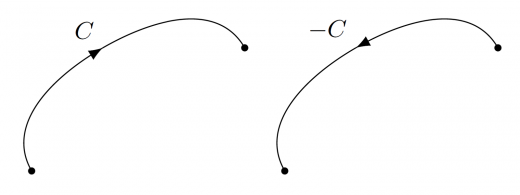
向きを逆にした曲線
曲線 を で定義されたなめらかな曲線とします。この曲線には に沿った向きが付いていることを注目しましょう。
の向きを逆にした曲線を で表し,文字通り「 を逆向きにたどった曲線」とします。すなわち によって定義される曲線を とします。
曲線の結合
2つのなめらかな曲線の和を定義します。
曲線 を で, を で定義されるなめらかな曲線とします。
特に の終点と の始点は同じとします。すなわち と仮定します。
このとき2曲線の結合 を の終点と の始点を繋げた曲線とします。すなわち によって定義される曲線を とします。

区分的になめらかな曲線
先ほどの のように「尖った」部分がある曲線や,単純なジグザグな折れ線などを経路とする積分はどう考えるべきでしょうか。ここで区分的になめらかという概念を導入します。
曲線 が,いくつかのなめらかな曲線の結合になっているとき,それを区分的になめらかな曲線といいます。
例えば先ほどの も虚部が正の部分と負の部分で分割することで,区分的になめらかな曲線となります。
積分の定義と性質
積分の定義と性質
(連続な)複素関数の積分を,これまでに定義した(区分的に)なめらかな曲線に沿った線積分として定義します。
なめらかな曲線上の積分
なめらかな曲線 が をパラメタとして により定められているとします。 上の連続関数 の積分を,(実積分に習い) と区間 を分割し,区分和 の極限として定義します。
を と実部・虚部に分けると,実積分の線積分として帰着できます。ゆえに は収束し と計算されます。
区分的になめらかな曲線上の積分
曲線 と区分的になめらかな曲線を,なめらかな曲線に分けましょう。このとき複素関数 の に沿った積分を次のように定めることができます。
複素積分の性質
複素積分には,実積分と同様に「線型性」が成り立ちます。
は連続な複素関数, を複素数, を区分的になめらかな曲線とする。このとき以下が成り立つ。
具体例
具体例
具体的な計算例を通して,複素積分を理解しましょう。
を次の経路に沿って積分せよ。
- 直線:
- 折れ線:
,ただし , とする。
を から まで積分をします。2通りの経路を考えましょう。
まずは,直線 に沿って積分します。
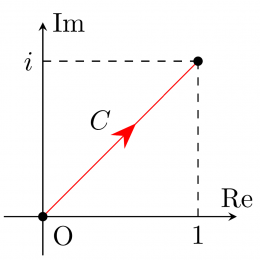
次は,折れ線 です。, により積分しましょう。

なんと,どちらも積分結果が同じになりました。実は,被積分関数 が正則である領域のなかでは積分結果は始点と終点だけで決まります!
を次の経路に沿って積分せよ。
を から まで積分をします。
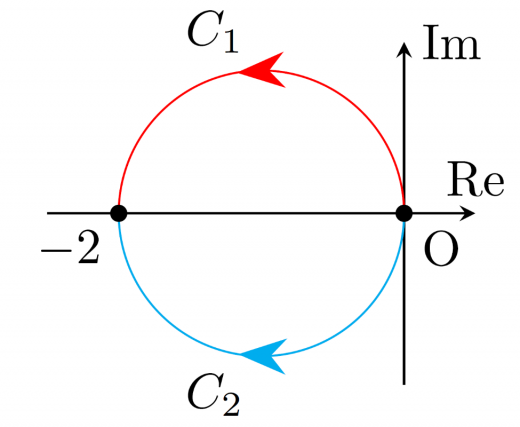
経路1
に沿って積分します。
経路2
に沿って積分します。
今回は積分結果が変わりました。
原始関数と積分
実積分のとき,原始関数を用いて積分を計算していました。同じようなことが複素積分でも成立します。
区分的になめらかな曲線 上で連続な関数 に, を含む領域で正則な関数 があって, 上で であるとき, である。
とおく。 である。よって が得られる。
この定理を踏まえて先ほどの例題を思い出しましょう。
には 全体で原始関数 が存在します。したがって積分経路によらず となったのです。
例2の場合, の原始関数は です。
となります。
複素数の対数関数とiのi乗の主値が実数であることの記事に詳しくは書いてありますが,複素数の範囲において の値は の分ズレが出てきて一意に定まりません。したがって積分の値にもズレが生じます。
積分路に寄って積分値が変わる例を見てきましたが,その根本的な原因はどこにあるのでしょうか。
例2の場合, が で正則ではないこと,すなわち で微積分できる関数ではないことが原因となっています。→コーシーリーマンの関係式と微分可能性・正則関数
積分路の変化については,より詳しく別の記事→ コーシーの積分定理と積分経路の変形で説明します。
複素積分の便利で美しい公式が今後登場していくのでお楽しみに!











