グルサの定理
コーシーの積分公式は,正則関数 f ( z ) f(z) f ( z ) f ( z ) f(z) f ( z ) n n n
グルサの定理(グルサの公式)
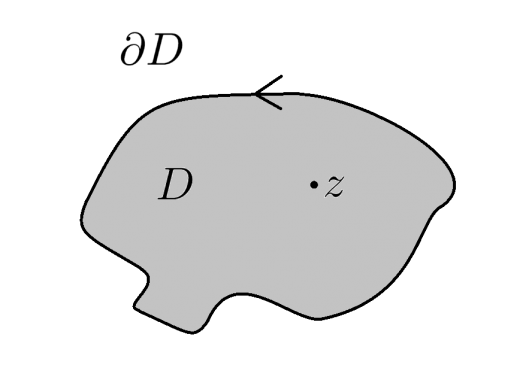
領域 D D D
f f f D ‾ = D ∪ ∂ D \overline{D} = D \cup \partial D D = D ∪ ∂ D
このとき D D D z z z
f ( n ) ( z ) = n ! 2 π i ∮ ∂ D f ( ζ ) ( ζ − z ) n + 1 d ζ
f^{(n)} (z) = \dfrac{n!}{2\pi i} \oint_{\partial D} \dfrac{f(\zeta)}{(\zeta - z)^{n+1}} \; d\zeta
f ( n ) ( z ) = 2 πi n ! ∮ ∂ D ( ζ − z ) n + 1 f ( ζ ) d ζ
となる。
n = 0 n=0 n = 0
正則(1階微分可能)なら,何回でも微分可能というのはすさまじい結果ですね。
系
正則関数 f f f f ′ f' f ′
この系によって,「関数 f f f F F F
グルサの定理の証明
帰納法によって証明します。簡単な極限計算だけで証明できます。
n = 1 n=1 n = 1 lim h → 0 f ( z + h ) − f ( z ) h = lim h → 0 1 h ( 1 2 π i ∮ ∂ D f ( ζ ) ζ − z − h d ζ − 1 2 π i ∮ ∂ D f ( ζ ) ζ − z d ζ ) = lim h → 0 1 h 1 2 π i ∮ ∂ D ( f ( ζ ) ζ − z − h − f ( ζ ) ζ − z ) d ζ = lim h → 0 1 h 1 2 π i ∮ ∂ D h ⋅ f ( ζ ) ( ζ − z − h ) ( ζ − z ) d ζ = lim h → 0 1 2 π i ∮ ∂ D f ( ζ ) ( ζ − z − h ) ( ζ − z ) d ζ \begin{aligned}
&\lim_{h \to 0} \dfrac{f(z+h)-f(z)}{h}\\
&= \lim_{h \to 0} \dfrac{1}{h} \left( \dfrac{1}{2\pi i} \oint_{\partial D} \dfrac{f(\zeta)}{\zeta - z - h} \; d\zeta - \dfrac{1}{2\pi i} \oint_{\partial D} \dfrac{f(\zeta)}{\zeta - z} \; d\zeta \right)\\
&=\lim_{h \to 0} \dfrac{1}{h} \dfrac{1}{2\pi i} \oint_{\partial D} \left( \dfrac{f(\zeta)}{\zeta - z - h} - \dfrac{f(\zeta)}{\zeta - z} \right) d\zeta\\
&=\lim_{h \to 0} \dfrac{1}{h} \dfrac{1}{2\pi i} \oint_{\partial D} \dfrac{h \cdot f(\zeta)}{(\zeta - z - h)(\zeta - z)} \; d\zeta\\
&=\lim_{h \to 0} \dfrac{1}{2\pi i} \oint_{\partial D} \dfrac{f(\zeta)}{(\zeta - z - h)(\zeta - z)} \; d\zeta
\end{aligned} h → 0 lim h f ( z + h ) − f ( z ) = h → 0 lim h 1 ( 2 πi 1 ∮ ∂ D ζ − z − h f ( ζ ) d ζ − 2 πi 1 ∮ ∂ D ζ − z f ( ζ ) d ζ ) = h → 0 lim h 1 2 πi 1 ∮ ∂ D ( ζ − z − h f ( ζ ) − ζ − z f ( ζ ) ) d ζ = h → 0 lim h 1 2 πi 1 ∮ ∂ D ( ζ − z − h ) ( ζ − z ) h ⋅ f ( ζ ) d ζ = h → 0 lim 2 πi 1 ∮ ∂ D ( ζ − z − h ) ( ζ − z ) f ( ζ ) d ζ 1 2 π i ∮ ∂ D f ( ζ ) ( ζ − z ) 2 d ζ
\dfrac{1}{2\pi i} \oint_{\partial D} \dfrac{f(\zeta)}{(\zeta - z)^2} \; d\zeta
2 πi 1 ∮ ∂ D ( ζ − z ) 2 f ( ζ ) d ζ ∣ ∮ ∂ D f ( ζ ) ( ζ − z − h ) ( ζ − z ) d ζ − ∮ ∂ D f ( ζ ) ( ζ − z ) 2 d ζ ∣ = ∣ ∮ ∂ D ( f ( ζ ) ( ζ − z − h ) ( ζ − z ) − f ( ζ ) ( ζ − z ) 2 ) d ζ ∣ = ∣ ∮ ∂ D h ⋅ f ( z ) ( ζ − z − h ) ( ζ − z ) 2 d ζ ∣ = ∣ ∮ ∂ D f ( z ) ( ζ − z − h ) ( ζ − z ) 2 d ζ ∣ ⋅ ∣ h ∣ \begin{aligned}
&\left| \oint_{\partial D} \dfrac{f(\zeta)}{(\zeta - z - h)(\zeta - z)} \; d\zeta - \oint_{\partial D} \dfrac{f(\zeta)}{(\zeta - z)^2} \; d\zeta \right|\\
&= \left| \oint_{\partial D} \left( \dfrac{f(\zeta)}{(\zeta - z - h)(\zeta - z)} -\dfrac{f(\zeta)}{(\zeta - z)^2} \right) \; d\zeta \right|\\
&= \left| \oint_{\partial D} \dfrac{h \cdot f(z)}{(\zeta - z - h)(\zeta - z)^2} \; d\zeta \right|\\
&= \left| \oint_{\partial D} \dfrac{f(z)}{(\zeta - z - h)(\zeta - z)^2} \; d\zeta \right| \cdot |h|
\end{aligned} ∣ ∣ ∮ ∂ D ( ζ − z − h ) ( ζ − z ) f ( ζ ) d ζ − ∮ ∂ D ( ζ − z ) 2 f ( ζ ) d ζ ∣ ∣ = ∣ ∣ ∮ ∂ D ( ( ζ − z − h ) ( ζ − z ) f ( ζ ) − ( ζ − z ) 2 f ( ζ ) ) d ζ ∣ ∣ = ∣ ∣ ∮ ∂ D ( ζ − z − h ) ( ζ − z ) 2 h ⋅ f ( z ) d ζ ∣ ∣ = ∣ ∣ ∮ ∂ D ( ζ − z − h ) ( ζ − z ) 2 f ( z ) d ζ ∣ ∣ ⋅ ∣ h ∣ h → 0 h \to 0 h → 0 0 0 0 lim h → 0 f ( z + h ) − f ( z ) h \displaystyle \lim_{h \to 0} \dfrac{f(z+h) - f(z)}{h} h → 0 lim h f ( z + h ) − f ( z ) f ( z ) f(z) f ( z ) f ′ ( z ) f'(z) f ′ ( z ) f ′ ( z ) = 1 2 π i ∮ ∂ D f ( ζ ) ( ζ − z ) 2 d ζ
f' (z) = \dfrac{1}{2\pi i} \oint_{\partial D} \dfrac{f(\zeta)}{(\zeta - z)^2} \; d\zeta
f ′ ( z ) = 2 πi 1 ∮ ∂ D ( ζ − z ) 2 f ( ζ ) d ζ
一般の n n n n − 1 n-1 n − 1 n = 1 n=1 n = 1 lim h → 0 f ( n − 1 ) ( z + h ) − f ( n − 1 ) ( z ) h = lim h → 0 1 h ( ( n − 1 ) ! 2 π i ∮ ∂ D f ( ζ ) ( ζ − z − h ) n d ζ − ( n − 1 ) ! 2 π i ∮ ∂ D f ( ζ ) ( ζ − z ) n d ζ ) = lim h → 0 1 h ( n − 1 ) ! 2 π i ∮ ∂ D { ( ζ − z ) n − ( ζ − z − h ) n } ⋅ f ( ζ ) ( ζ − z − h ) n ( ζ − z ) n d ζ = lim h → 0 1 h ( n − 1 ) ! 2 π i ∮ ∂ D { n h ( ζ − z ) n − 1 + O ( h 2 ) } ⋅ f ( ζ ) ( ζ − z − h ) n ( ζ − z ) n d ζ = lim h → 0 n ! 2 π i ∮ ∂ D f ( ζ ) ( ζ − z − h ) n ( ζ − z ) d ζ \begin{aligned}
&\lim_{h \to 0} \dfrac{f^{(n-1)} (z+h) - f^{(n-1)} (z)}{h}\\
&= \lim_{h \to 0} \dfrac{1}{h} \left( \dfrac{(n-1)!}{2\pi i} \oint_{\partial D} \dfrac{f(\zeta)}{(\zeta - z - h)^{n}} \; d\zeta - \dfrac{(n-1)!}{2\pi i} \oint_{\partial D} \dfrac{f(\zeta)}{(\zeta - z)^{n}} \; d\zeta \right)\\
&= \lim_{h \to 0} \dfrac{1}{h} \dfrac{(n-1)!}{2\pi i} \oint_{\partial D} \dfrac{\{ (\zeta - z)^{n} - (\zeta - z - h)^{n} \} \cdot f(\zeta)}{(\zeta - z - h)^{n} (\zeta - z)^{n}} \; d\zeta\\
&= \lim_{h \to 0} \dfrac{1}{h} \dfrac{(n-1)!}{2\pi i} \oint_{\partial D} \dfrac{\{ nh(\zeta-z)^{n-1} + O(h^2) \} \cdot f(\zeta)}{(\zeta - z - h)^{n} (\zeta - z)^{n}} \; d\zeta\\
&= \lim_{h \to 0} \dfrac{n!}{2\pi i} \oint_{\partial D} \dfrac{f(\zeta)}{(\zeta - z - h)^{n} (\zeta - z)} \; d\zeta
\end{aligned} h → 0 lim h f ( n − 1 ) ( z + h ) − f ( n − 1 ) ( z ) = h → 0 lim h 1 ( 2 πi ( n − 1 )! ∮ ∂ D ( ζ − z − h ) n f ( ζ ) d ζ − 2 πi ( n − 1 )! ∮ ∂ D ( ζ − z ) n f ( ζ ) d ζ ) = h → 0 lim h 1 2 πi ( n − 1 )! ∮ ∂ D ( ζ − z − h ) n ( ζ − z ) n {( ζ − z ) n − ( ζ − z − h ) n } ⋅ f ( ζ ) d ζ = h → 0 lim h 1 2 πi ( n − 1 )! ∮ ∂ D ( ζ − z − h ) n ( ζ − z ) n { nh ( ζ − z ) n − 1 + O ( h 2 )} ⋅ f ( ζ ) d ζ = h → 0 lim 2 πi n ! ∮ ∂ D ( ζ − z − h ) n ( ζ − z ) f ( ζ ) d ζ O ( h 2 ) O(h^2) O ( h 2 ) ランダウの記号 とする。最後の極限も n = 1 n=1 n = 1 1 2 π i ∮ ∂ D f ( ζ ) ( ζ − z ) n − 1 d ζ
\dfrac{1}{2\pi i} \oint_{\partial D} \dfrac{f(\zeta)}{(\zeta - z)^{n-1}} \; d\zeta
2 πi 1 ∮ ∂ D ( ζ − z ) n − 1 f ( ζ ) d ζ lim h → 0 f ( n − 1 ) ( z + h ) − f ( n − 1 ) ( z ) h \displaystyle \lim_{h \to 0} \dfrac{f^{(n-1)} (z+h) - f^{(n-1)} (z)}{h} h → 0 lim h f ( n − 1 ) ( z + h ) − f ( n − 1 ) ( z ) f ( z ) f(z) f ( z ) n n n f ( n ) ( z ) f^{(n)} (z) f ( n ) ( z ) f ( n ) ( z ) = n ! 2 π i ∮ ∂ D f ( ζ ) ( ζ − z ) n + 1 d ζ
f^{(n)} (z) = \dfrac{n!}{2\pi i} \oint_{\partial D} \dfrac{f(\zeta)}{(\zeta - z)^{n+1}} \; d\zeta
f ( n ) ( z ) = 2 πi n ! ∮ ∂ D ( ζ − z ) n + 1 f ( ζ ) d ζ
例題
例題
領域 D D D { f n } \{ f_n \} { f n } f f f { f n ′ } \{ f'_n \} { f n ′ } f ′ f' f ′
ただし広義一様収束 とは,任意のコンパクト集合上で一様収束 することを意味します(今回の場合は任意の閉円盤上で一様収束することが必要十分です)。
解
z 0 ∈ C , R ∈ R > 0 z_0 \in \mathbb{C} , R \in \mathbb{R}_{>0} z 0 ∈ C , R ∈ R > 0 Δ ( z 0 , R ) ⊂ D \Delta (z_0,R) \subset D Δ ( z 0 , R ) ⊂ D
Δ ( z 0 , R ) \Delta (z_0 , R) Δ ( z 0 , R ) ε > 0 \varepsilon > 0 ε > 0 n n n sup z ∈ Δ ( z 0 , R ) ∣ f n ′ ( z ) − f ′ ( z ) ∣ < ε \sup_{z \in \Delta (z_0,R)} |f_n' (z) - f'(z)| < \varepsilon sup z ∈ Δ ( z 0 , R ) ∣ f n ′ ( z ) − f ′ ( z ) ∣ < ε
Δ ( z 0 , R ) \Delta (z_0 , R) Δ ( z 0 , R ) z z z D D D r > 0 r > 0 r > 0 Δ ( z 0 , R + r ) ⊂ D \Delta (z_0 , R + r) \subset D Δ ( z 0 , R + r ) ⊂ D f n f_n f n D D D Δ ( z 0 , R + r ) \Delta (z_0 , R + r) Δ ( z 0 , R + r ) n n n sup z ∈ Δ ( z 0 , R + r ) ∣ f n ( z ) − f ( z ) ∣ < ε \sup_{z \in \Delta (z_0 , R+r)} |f_n (z) - f (z)| < \varepsilon sup z ∈ Δ ( z 0 , R + r ) ∣ f n ( z ) − f ( z ) ∣ < ε
グルサの定理より
f n ′ ( z ) = 1 2 π i ∮ ∂ Δ ( z , r ) f n ( ζ ) ( ζ − z ) 2 d ζ f ′ ( z ) = 1 2 π i ∮ ∂ Δ ( z , r ) f ( ζ ) ( ζ − z ) 2 d ζ
f'_n (z) = \dfrac{1}{2\pi i} \oint_{\partial \Delta (z,r)} \dfrac{f_n(\zeta)}{(\zeta - z)^{2}} \; d\zeta\\
f' (z) = \dfrac{1}{2\pi i} \oint_{\partial \Delta (z,r)} \dfrac{f(\zeta)}{(\zeta - z)^{2}} \; d\zeta
f n ′ ( z ) = 2 πi 1 ∮ ∂ Δ ( z , r ) ( ζ − z ) 2 f n ( ζ ) d ζ f ′ ( z ) = 2 πi 1 ∮ ∂ Δ ( z , r ) ( ζ − z ) 2 f ( ζ ) d ζ
n n n ∣ f n ′ ( z ) − f ′ ( z ) ∣ = ∣ 1 2 π i ∮ ∂ Δ ( z , r ) f n ( ζ ) ( ζ − z ) 2 d ζ − 1 2 π i ∮ ∂ Δ ( z , r ) f ( ζ ) ( ζ − z ) 2 d ζ ∣ = ∣ 1 2 π i ∮ ∂ Δ ( z , r ) f n ( ζ ) − f ( ζ ) ( ζ − z ) 2 d ζ ∣ = 1 2 π r 2 ∮ ∂ Δ ( z , r ) ∣ f n ( ζ ) − f ( ζ ) ∣ d ζ ≦ 1 2 π r 2 ∮ ∂ Δ ( z , r ) sup ζ ∈ Δ ( z 0 , R + r ) ∣ f n ( ζ ) − f ( ζ ) ∣ d ζ = 1 2 π r 2 ⋅ 2 π r 2 ⋅ ε = ε \begin{aligned}
&|f_n' (z) - f'(z)|\\
&= \left| \dfrac{1}{2\pi i} \oint_{\partial \Delta (z,r)} \dfrac{f_n(\zeta)}{(\zeta - z)^{2}} \; d\zeta - \dfrac{1}{2\pi i} \oint_{\partial \Delta (z,r)} \dfrac{f(\zeta)}{(\zeta - z)^{2}} \; d\zeta \right|\\
&= \left| \dfrac{1}{2\pi i} \oint_{\partial \Delta (z,r)} \dfrac{f_n(\zeta) - f(\zeta)}{(\zeta - z)^{2}} \; d\zeta \right|\\
&= \dfrac{1}{2\pi r^2} \oint_{\partial \Delta (z,r)} |f_n (\zeta) - f(\zeta)| \; d\zeta\\
&\leqq \dfrac{1}{2\pi r^2} \oint_{\partial \Delta (z,r)} \sup_{\zeta \in \Delta (z_0 , R+r)} |f_n (\zeta) - f(\zeta)| \; d\zeta\\
&= \dfrac{1}{2\pi r^2} \cdot 2\pi r^2 \cdot \varepsilon = \varepsilon
\end{aligned} ∣ f n ′ ( z ) − f ′ ( z ) ∣ = ∣ ∣ 2 πi 1 ∮ ∂ Δ ( z , r ) ( ζ − z ) 2 f n ( ζ ) d ζ − 2 πi 1 ∮ ∂ Δ ( z , r ) ( ζ − z ) 2 f ( ζ ) d ζ ∣ ∣ = ∣ ∣ 2 πi 1 ∮ ∂ Δ ( z , r ) ( ζ − z ) 2 f n ( ζ ) − f ( ζ ) d ζ ∣ ∣ = 2 π r 2 1 ∮ ∂ Δ ( z , r ) ∣ f n ( ζ ) − f ( ζ ) ∣ d ζ ≦ 2 π r 2 1 ∮ ∂ Δ ( z , r ) ζ ∈ Δ ( z 0 , R + r ) sup ∣ f n ( ζ ) − f ( ζ ) ∣ d ζ = 2 π r 2 1 ⋅ 2 π r 2 ⋅ ε = ε sup z ∈ Δ ( z 0 , R ) ∣ f n ′ ( z ) − f ′ ( z ) ∣ < ε
\sup_{z \in \Delta (z_0,R)} |f_n' (z) - f'(z)| < \varepsilon
z ∈ Δ ( z 0 , R ) sup ∣ f n ′ ( z ) − f ′ ( z ) ∣ < ε f n ′ f_n' f n ′ f ′ f' f ′
このようにグルサの定理を用いることで,微分の不等式を積分により評価する ことができます。
こうした評価は
正則関数の積分は積分経路を自由に変形できる
元の関数の評価を活用できる
ことから非常に重要かつ有用なテクニックです。
モレラの定理
コーシーの積分定理 を思い出しましょう。領域 D D D f ( z ) f(z) f ( z ) D D D C C C 0 0 0
逆はどうでしょうか?つまり,単純閉曲線 C C C 0 0 0 モレラの定理 はこの問いの答えとなります。
モレラの定理
領域 D D D f f f D D D C C C ∮ C f ( z ) d z = 0
\oint_{C} f(z) \; dz = 0
∮ C f ( z ) d z = 0 f f f D D D
具体例1:ガンマ関数
モレラの定理を用いていくつかの関数が正則であることを証明しましょう。
ガンマ関数 は,
Γ ( z ) = ∫ 0 ∞ t z − 1 e − t d t
\Gamma(z)= \int_0^{\infty} t^{z-1} e^{-t}dt
Γ ( z ) = ∫ 0 ∞ t z − 1 e − t d t
ガンマ関数が D = { z ∈ C ∣ R e ( z ) > 0 } D = \{ z \in \mathbb{C} \mid \mathrm{Re} (z) > 0 \} D = { z ∈ C ∣ Re ( z ) > 0 }
D D D C C C ∮ C Γ ( z ) d z = ∮ C ∫ 0 ∞ t z − 1 e − t d t d z
\oint_{C} \Gamma (z) \; dz = \oint_{C} \int_0^{\infty} t^{z-1} e^{-t}dt dz
∮ C Γ ( z ) d z = ∮ C ∫ 0 ∞ t z − 1 e − t d t d z ∮ C Γ ( z ) d z = ∮ C ∫ 0 ∞ t z − 1 e − t d t d z = ∫ 0 ∞ e − t ( ∮ C t z − 1 d z ) d t = 0 \begin{aligned}
\oint_{C} \Gamma (z) \; dz &= \oint_{C} \int_0^{\infty} t^{z-1} e^{-t}dt dz\\
&= \int_0^{\infty} e^{-t} \left( \oint_{C} t^{z-1} dz \right) dt\\
&= 0
\end{aligned} ∮ C Γ ( z ) d z = ∮ C ∫ 0 ∞ t z − 1 e − t d t d z = ∫ 0 ∞ e − t ( ∮ C t z − 1 d z ) d t = 0 t x − 1 t^{x-1} t x − 1 D D D
こうしてモレラの定理から正則になります。
具体例2:ゼータ関数
ゼータ関数 は,
ζ ( s ) = ∑ n = 1 ∞ 1 n s
\zeta (s) = \sum_{n=1}^{\infty} \dfrac{1}{n^s}
ζ ( s ) = n = 1 ∑ ∞ n s 1
ゼータ関数が D = { z ∈ C ∣ R e ( z ) > 1 } D = \{ z \in \mathbb{C} \mid \mathrm{Re} (z) > 1 \} D = { z ∈ C ∣ Re ( z ) > 1 }
D D D C C C
∮ C ζ ( s ) d s = ∮ C ∑ n = 1 ∞ 1 n s d s
\oint_{C} \zeta (s) \; ds = \oint_{C} \sum_{n=1}^{\infty} \dfrac{1}{n^s} \; ds
∮ C ζ ( s ) d s = ∮ C n = 1 ∑ ∞ n s 1 d s ワイエルシュトラスのM判定法 より,積分と極限を入れ替えることができて,
∮ C ζ ( s ) d s = ∑ n = 1 ∞ ∮ C 1 n s d s
\oint_{C} \zeta (s) \; ds = \sum_{n=1}^{\infty} \oint_{C} \dfrac{1}{n^s} \; ds
∮ C ζ ( s ) d s = n = 1 ∑ ∞ ∮ C n s 1 d s 1 n s \dfrac{1}{n^s} n s 1 D D D 0 0 0 ∮ C ζ ( s ) d s = 0
\oint_{C} \zeta (s) \; ds = 0
∮ C ζ ( s ) d s = 0 ζ ( s ) \zeta (s) ζ ( s ) D D D
モレラの定理の証明
証明
以下では,単に曲線と書いた場合,D D D
1点 a a a Γ z \Gamma_z Γ z a a a z z z F ( z ) = ∫ Γ z f ( ζ ) d ζ
F(z) = \int_{\Gamma_z} f(\zeta) \; d\zeta
F ( z ) = ∫ Γ z f ( ζ ) d ζ F ( z ) F(z) F ( z ) Γ z ′ \Gamma_z' Γ z ′ a a a z z z a a a z z z Γ z − Γ z ′ \Gamma_z - \Gamma_z' Γ z − Γ z ′ ∮ Γ z − Γ z ′ f ( ζ ) d ζ = 0
\oint_{\Gamma_z - \Gamma_z'} f(\zeta) \; d\zeta = 0
∮ Γ z − Γ z ′ f ( ζ ) d ζ = 0 ∮ Γ z f ( ζ ) d ζ = ∮ Γ z ′ f ( ζ ) d ζ + ∮ Γ z − Γ z ′ f ( ζ ) d ζ = ∮ Γ z ′ f ( ζ ) d ζ
\oint_{\Gamma_z} f(\zeta) \; d\zeta = \oint_{\Gamma_z'} f(\zeta) \; d\zeta + \oint_{\Gamma_z - \Gamma_z'} f(\zeta) \; d\zeta =\oint_{\Gamma_z'} f(\zeta) \; d\zeta
∮ Γ z f ( ζ ) d ζ = ∮ Γ z ′ f ( ζ ) d ζ + ∮ Γ z − Γ z ′ f ( ζ ) d ζ = ∮ Γ z ′ f ( ζ ) d ζ Γ z \Gamma_z Γ z F ( z ) F(z) F ( z ) Γ z \Gamma_z Γ z a a a z z z
F ′ ( z ) = f ( z ) F'(z) = f(z) F ′ ( z ) = f ( z ) ε > 0 \varepsilon > 0 ε > 0 f f f δ \delta δ ∣ ζ − z ∣ < δ |\zeta - z| < \delta ∣ ζ − z ∣ < δ ζ \zeta ζ ∣ f ( ζ ) − f ( z ) ∣ < ε |f(\zeta) - f(z)| < \varepsilon ∣ f ( ζ ) − f ( z ) ∣ < ε
h h h 0 0 0 ∣ h ∣ < δ |h| < \delta ∣ h ∣ < δ
L z , z + h L_{z,z+h} L z , z + h z z z z + h z+h z + h z z z z + h z+h z + h Γ z + L z , z + h − Γ z + h \Gamma_z + L_{z,z+h} - \Gamma_{z+h} Γ z + L z , z + h − Γ z + h a , z , z + h a,z,z+h a , z , z + h
よって仮定から
∮ Γ z + L z , z + h − Γ z + h f ( z ) d z = 0
\oint_{\Gamma_z + L_{z,z+h} - \Gamma_{z+h}} f(z) \; dz = 0
∮ Γ z + L z , z + h − Γ z + h f ( z ) d z = 0 ∮ L z , z + h f ( z ) d z = ∮ Γ z + h − Γ z f ( z ) d z = F ( z + h ) − F ( z ) \begin{aligned}
\oint_{L_{z,z+h}} f(z) \; dz &= \oint_{\Gamma_{z+h} - \Gamma_z} f(z) \; dz\\
&= F(z+h) - F(z)
\end{aligned} ∮ L z , z + h f ( z ) d z = ∮ Γ z + h − Γ z f ( z ) d z = F ( z + h ) − F ( z )
∣ F ( z + h ) − F ( z ) h − f ( z ) ∣ = ∣ 1 h ∮ L z , z + h f ( ζ ) d ζ − f ( z ) ∣ = ∣ 1 h ∮ L z , z + h ( f ( ζ ) − f ( z ) ) d ζ ∣ ≦ 1 h ∮ L z , z + h ∣ f ( ζ ) − f ( z ) ∣ d ζ ≦ 1 h ∮ L z , z + h sup ∣ ζ − z ∣ ≦ ∣ h ∣ ∣ f ( ζ ) − f ( z ) ∣ d ζ = sup ∣ ζ − z ∣ ≦ ∣ h ∣ ∣ f ( ζ ) − f ( z ) ∣ \begin{aligned}
&\left| \dfrac{F(z+h) - F(z)}{h} - f(z) \right|\\
&= \left| \dfrac{1}{h} \oint_{L_{z,z+h}} f(\zeta) \; d\zeta - f(z) \right|\\
&= \left| \dfrac{1}{h} \oint_{L_{z,z+h}} (f(\zeta) - f(z)) \; d\zeta \right|\\
&\leqq \dfrac{1}{h} \oint_{L_{z,z+h}} |f(\zeta) - f(z)| \; d\zeta\\
&\leqq \dfrac{1}{h} \oint_{L_{z,z+h}} \sup_{|\zeta - z| \leqq |h|} |f(\zeta) - f(z)| \; d\zeta\\
&= \sup_{|\zeta - z| \leqq |h|} |f(\zeta) - f(z)|
\end{aligned} ∣ ∣ h F ( z + h ) − F ( z ) − f ( z ) ∣ ∣ = ∣ ∣ h 1 ∮ L z , z + h f ( ζ ) d ζ − f ( z ) ∣ ∣ = ∣ ∣ h 1 ∮ L z , z + h ( f ( ζ ) − f ( z )) d ζ ∣ ∣ ≦ h 1 ∮ L z , z + h ∣ f ( ζ ) − f ( z ) ∣ d ζ ≦ h 1 ∮ L z , z + h ∣ ζ − z ∣ ≦ ∣ h ∣ sup ∣ f ( ζ ) − f ( z ) ∣ d ζ = ∣ ζ − z ∣ ≦ ∣ h ∣ sup ∣ f ( ζ ) − f ( z ) ∣
h h h sup ∣ ζ − z ∣ ≦ ∣ h ∣ ∣ f ( ζ ) − f ( z ) ∣ < ε \displaystyle \sup_{|\zeta - z| \leqq |h|} |f(\zeta) - f(z)| < \varepsilon ∣ ζ − z ∣ ≦ ∣ h ∣ sup ∣ f ( ζ ) − f ( z ) ∣ < ε lim h → 0 F ( z + h ) − F ( z ) h = f ( z )
\lim_{h \to 0} \dfrac{F(z+h) - F(z)}{h} = f(z)
h → 0 lim h F ( z + h ) − F ( z ) = f ( z ) F F F F F F f f f
前述したように正則な原始関数を用意することで,f f f