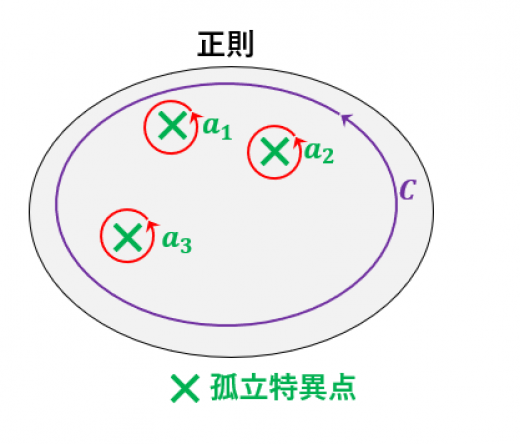
留数定理:1 2 π i ∮ C f ( z ) d z = ∑ i = 1 n R e s ( f , a i ) \displaystyle\dfrac{1}{2\pi i} \oint_{C} f(z) \; dz = \sum_{i=1}^n \mathrm{Res} (f , a_i) 2 πi 1 ∮ C f ( z ) d z = i = 1 ∑ n Res ( f , a i ) 留数 R e s ( f , a i ) \mathrm{Res} (f , a_i) Res ( f , a i ) という嬉しい定理です。
留数定理を用いた留数計算
留数定理を駆使することで逆に留数を計算することもできます。
例題
e 1 z z 2 + 1 \dfrac{e^{\frac{1}{z}}}{z^2+1} z 2 + 1 e z 1 z = 0 z=0 z = 0
ローラン展開を用いた計算
まずはローラン展開を計算してみます。
e 1 z z 2 + 1 = ( 1 + 1 z + 1 2 z 2 ⋯ ) ( 1 + ( − z 2 ) + ( − z 2 ) 2 + ⋯ ) \begin{aligned}
\dfrac{e^{\frac{1}{z}}}{z^2+1} &= \left( 1 + \dfrac{1}{z} + \dfrac{1}{2z^2} \cdots \right) \left( 1 + (-z^2) + (-z^2)^2 + \cdots \right)\\
\end{aligned} z 2 + 1 e z 1 = ( 1 + z 1 + 2 z 2 1 ⋯ ) ( 1 + ( − z 2 ) + ( − z 2 ) 2 + ⋯ )
このうち z − 1 z^{-1} z − 1 1 z ⋅ 1 + 1 3 ! z 3 ⋅ ( − z 2 ) + 1 5 ! z 5 ⋅ ( − z 2 ) 2 + ⋯
\dfrac{1}{z} \cdot 1 + \dfrac{1}{3! z^3} \cdot (-z^2) + \dfrac{1}{5! z^5} \cdot (-z^2)^2 + \cdots
z 1 ⋅ 1 + 3 ! z 3 1 ⋅ ( − z 2 ) + 5 ! z 5 1 ⋅ ( − z 2 ) 2 + ⋯ 1 − 1 3 ! + 1 5 ! + ⋯ = sin 1
1 - \dfrac{1}{3!} + \dfrac{1}{5!} + \cdots = \sin 1
1 − 3 ! 1 + 5 ! 1 + ⋯ = sin 1 R e s ( e 1 z z 2 + 1 , 0 ) = sin 1
\mathrm{Res} \left( \dfrac{e^{\frac{1}{z}}}{z^2+1} , 0 \right) = \sin 1
Res ( z 2 + 1 e z 1 , 0 ) = sin 1
留数定理を用いた計算
e 1 z z 2 + 1 \dfrac{e^{\frac{1}{z}}}{z^2+1} z 2 + 1 e z 1 z = 0 , ± i z = 0, \pm i z = 0 , ± i R R R 0 , ± i ∈ Δ ( 0 , R ) 0 , \pm i \in \Delta (0,R) 0 , ± i ∈ Δ ( 0 , R )
このとき 留数定理 から
1 2 π i ∮ Δ ( 0 , R ) e 1 z z 2 + 1 d z = R e s ( e 1 z z 2 + 1 , 0 ) + R e s ( e 1 z z 2 + 1 , i ) + R e s ( e 1 z z 2 + 1 , − i ) \begin{aligned}
&\dfrac{1}{2\pi i} \oint_{\Delta (0,R)} \dfrac{e^{\frac{1}{z}}}{z^2+1} dz\\
&= \mathrm{Res} \left( \dfrac{e^{\frac{1}{z}}}{z^2+1} , 0 \right) + \mathrm{Res} \left( \dfrac{e^{\frac{1}{z}}}{z^2+1} , i \right) + \mathrm{Res} \left( \dfrac{e^{\frac{1}{z}}}{z^2+1} , -i \right)
\end{aligned} 2 πi 1 ∮ Δ ( 0 , R ) z 2 + 1 e z 1 d z = Res ( z 2 + 1 e z 1 , 0 ) + Res ( z 2 + 1 e z 1 , i ) + Res ( z 2 + 1 e z 1 , − i ) R R R
R e s ( e 1 z z 2 + 1 , i ) = lim z → i e 1 z z + i = e 1 i 2 i = e − i 2 i \begin{aligned}
\mathrm{Res} \left( \dfrac{e^{\frac{1}{z}}}{z^2+1} , i \right) &= \lim_{z \to i} \dfrac{e^{\frac{1}{z}}}{z+i}\\
&= \dfrac{e^{\frac{1}{i}}}{2i}\\
&= \dfrac{e^{-i}}{2i}
\end{aligned} Res ( z 2 + 1 e z 1 , i ) = z → i lim z + i e z 1 = 2 i e i 1 = 2 i e − i R e s ( e 1 z z 2 + 1 , i ) + R e s ( e 1 z z 2 + 1 , − i ) = e − i 2 i − e i 2 i = − sin 1 \begin{aligned}
\mathrm{Res} \left( \dfrac{e^{\frac{1}{z}}}{z^2+1} , i \right) + \mathrm{Res} \left( \dfrac{e^{\frac{1}{z}}}{z^2+1} , -i \right) &= \dfrac{e^{-i}}{2i} - \dfrac{e^{i}}{2i}\\
&= -\sin 1
\end{aligned} Res ( z 2 + 1 e z 1 , i ) + Res ( z 2 + 1 e z 1 , − i ) = 2 i e − i − 2 i e i = − sin 1
ここで
lim R → ∞ ∣ ∮ Δ ( 0 , R ) e 1 z z 2 + 1 d z ∣ ≦ lim R → ∞ ∮ Δ ( 0 , R ) ∣ e 1 z ∣ ∣ z 2 + 1 ∣ d z ≦ lim R → ∞ ∮ Δ ( 0 , R ) e 1 R R 2 − 1 d z = 0 \begin{aligned}
\lim_{R \to \infty} \left| \oint_{\Delta (0,R)} \dfrac{e^{\frac{1}{z}}}{z^2+1} dz \right| &\leqq \lim_{R \to \infty} \oint_{\Delta (0,R)} \dfrac{|e^{\frac{1}{z}}|}{|z^2+1|} dz\\
&\leqq \lim_{R \to \infty} \oint_{\Delta (0,R)} \dfrac{e^{\frac{1}{R}}}{R^2-1} dz \\
&= 0
\end{aligned} R → ∞ lim ∣ ∣ ∮ Δ ( 0 , R ) z 2 + 1 e z 1 d z ∣ ∣ ≦ R → ∞ lim ∮ Δ ( 0 , R ) ∣ z 2 + 1∣ ∣ e z 1 ∣ d z ≦ R → ∞ lim ∮ Δ ( 0 , R ) R 2 − 1 e R 1 d z = 0 R → ∞ R \to \infty R → ∞ 0 = R e s ( e 1 z z 2 + 1 , 0 ) + R e s ( e 1 z z 2 + 1 , i ) + R e s ( e 1 z z 2 + 1 , − i ) = R e s ( e 1 z z 2 + 1 , 0 ) − sin 1 \begin{aligned}
0 &= \mathrm{Res} \left( \dfrac{e^{\frac{1}{z}}}{z^2+1} , 0 \right) + \mathrm{Res} \left( \dfrac{e^{\frac{1}{z}}}{z^2+1} , i \right) + \mathrm{Res} \left( \dfrac{e^{\frac{1}{z}}}{z^2+1} , -i \right)\\
&= \mathrm{Res} \left( \dfrac{e^{\frac{1}{z}}}{z^2+1} , 0 \right) -\sin 1
\end{aligned} 0 = Res ( z 2 + 1 e z 1 , 0 ) + Res ( z 2 + 1 e z 1 , i ) + Res ( z 2 + 1 e z 1 , − i ) = Res ( z 2 + 1 e z 1 , 0 ) − sin 1 R e s ( e 1 z z 2 + 1 , 0 ) = sin 1
\mathrm{Res} \left( \dfrac{e^{\frac{1}{z}}}{z^2+1} , 0 \right) = \sin 1
Res ( z 2 + 1 e z 1 , 0 ) = sin 1
このように十分大きな R R R R → ∞ R \to \infty R → ∞
留数定理による実積分
留数定理は複素関数の積分に関する定理ですが,以下のように実積分を計算するのにも役立ちます!
例題
∫ − ∞ ∞ d x x 4 + 1 \displaystyle \int_{-\infty}^{\infty} \dfrac{dx}{x^4+1} ∫ − ∞ ∞ x 4 + 1 d x
実積分を留数定理を使って解くステップは次のようになります。
[ − R , R ] [-R,R] [ − R , R ] [ 0 , R ] [0,R] [ 0 , R ] C C C このとき,極が囲われた領域に入るように閉曲線を調整する。
留数定理を用いて C C C
R → ∞ R \to \infty R → ∞
解
実数 R > 0 R > 0 R > 0
C 1 C_1 C 1 ( − R , 0 ) (-R,0) ( − R , 0 ) ( R , 0 ) (R,0) ( R , 0 ) C 2 C_2 C 2 x 2 + y 2 = R 2 x^2+y^2=R^2 x 2 + y 2 = R 2 x ≧ 0 x \geqq 0 x ≧ 0 C = C 1 + C 2 C = C_1 + C_2 C = C 1 + C 2
1 z 4 + 1 \dfrac{1}{z^4+1} z 4 + 1 1 1 ± i 2 , − 1 ± i 2 \dfrac{1 \pm i}{\sqrt{2}} , \dfrac{-1 \pm i}{\sqrt{2}} 2 1 ± i , 2 − 1 ± i 1 1 1 R R R ± 1 + i 2 \dfrac{\pm 1 + i}{\sqrt{2}} 2 ± 1 + i C C C
よって留数定理 から
∮ C d z z 4 + 1 = 2 π i { R e s ( 1 z 4 + 1 , − 1 + i 2 ) + R e s ( 1 z 4 + 1 , 1 + i 2 ) }
\oint_{C} \dfrac{dz}{z^4+1} = 2 \pi i \left\{ \mathrm{Res} \left( \dfrac{1}{z^4+1} , \dfrac{-1+i}{\sqrt{2}} \right) + \mathrm{Res} \left( \dfrac{1}{z^4+1} , \dfrac{1+i}{\sqrt{2}} \right) \right\}
∮ C z 4 + 1 d z = 2 πi { Res ( z 4 + 1 1 , 2 − 1 + i ) + Res ( z 4 + 1 1 , 2 1 + i ) }
である。
R e s ( 1 z 4 + 1 , − 1 + i 2 ) = lim z → − 1 + i 2 ( z − − 1 + i 2 ) 1 z 4 + 1 = lim z → − 1 + i 2 1 ( z − 1 + i 2 ) ( z − 1 − i 2 ) ( z − − 1 − i 2 ) = 1 ( − 1 + i 2 − 1 + i 2 ) ( − 1 + i 2 − 1 − i 2 ) ( − 1 + i 2 − − 1 − i 2 ) = 1 − 2 ⋅ 2 ( i − 1 ) ⋅ 2 i = 1 − i 4 2 \begin{aligned}
&\mathrm{Res} \left( \dfrac{1}{z^4+1} ,\dfrac{-1+i}{\sqrt{2}} \right)\\
&= \lim_{z \to \frac{-1+i}{\sqrt{2}}} \left( z - \dfrac{-1+i}{\sqrt{2}} \right) \dfrac{1}{z^4+1}\\
&= \lim_{z \to \frac{-1+i}{\sqrt{2}}} \dfrac{1}{\left( z-\frac{1+i}{\sqrt{2}} \right) \left( z-\frac{1-i}{\sqrt{2}} \right) \left( z-\frac{-1-i}{\sqrt{2}} \right)}\\
&= \dfrac{1}{\left( \frac{-1+i}{\sqrt{2}} - \frac{1+i}{\sqrt{2}} \right) \left( \frac{-1+i}{\sqrt{2}} - \frac{1-i}{\sqrt{2}} \right) \left( \frac{-1+i}{\sqrt{2}} - \frac{-1-i}{\sqrt{2}} \right)}\\
&= \dfrac{1}{-\sqrt{2} \cdot \sqrt{2} (i-1) \cdot \sqrt{2} i}\\
&= \dfrac{1-i}{4\sqrt{2}}
\end{aligned} Res ( z 4 + 1 1 , 2 − 1 + i ) = z → 2 − 1 + i lim ( z − 2 − 1 + i ) z 4 + 1 1 = z → 2 − 1 + i lim ( z − 2 1 + i ) ( z − 2 1 − i ) ( z − 2 − 1 − i ) 1 = ( 2 − 1 + i − 2 1 + i ) ( 2 − 1 + i − 2 1 − i ) ( 2 − 1 + i − 2 − 1 − i ) 1 = − 2 ⋅ 2 ( i − 1 ) ⋅ 2 i 1 = 4 2 1 − i
同様にして
R e s ( 1 z 4 + 1 , 1 + i 2 ) = − 1 − i 4 2
\mathrm{Res} \left( \dfrac{1}{z^4+1} ,\dfrac{1+i}{\sqrt{2}} \right) = \dfrac{-1-i}{4\sqrt{2}}
Res ( z 4 + 1 1 , 2 1 + i ) = 4 2 − 1 − i ∮ C d z z 4 + 1 = 2 π i ( 1 − i 4 2 + − 1 − i 4 2 ) = π 2 \begin{aligned}
&\oint_{C} \dfrac{dz}{z^4+1}\\
&= 2 \pi i \left( \dfrac{1-i}{4\sqrt{2}} + \dfrac{-1-i}{4\sqrt{2}} \right)\\
&= \dfrac{\pi}{\sqrt{2}}
\end{aligned} ∮ C z 4 + 1 d z = 2 πi ( 4 2 1 − i + 4 2 − 1 − i ) = 2 π
上の結果は R R R lim R → ∞ ∮ C d z z 4 + 1 = π 2
\lim_{R \to \infty} \oint_{C} \dfrac{dz}{z^4+1} = \dfrac{\pi}{\sqrt{2}}
R → ∞ lim ∮ C z 4 + 1 d z = 2 π
次に C 1 , C 2 C_1,C_2 C 1 , C 2
lim R → ∞ ∫ C 1 d z z 4 + 1 = ∫ − ∞ ∞ d x x 4 + 1
\lim_{R \to \infty} \int_{C_1} \dfrac{dz}{z^4+1} = \int_{-\infty}^{\infty} \dfrac{dx}{x^4+1}
R → ∞ lim ∫ C 1 z 4 + 1 d z = ∫ − ∞ ∞ x 4 + 1 d x ∣ lim R → ∞ ∫ C 2 d z z 4 + 1 ∣ ≦ lim R → ∞ ∫ C 2 ∣ d z ∣ ∣ z 4 + 1 ∣ ≦ lim R → ∞ ∫ 0 π R R 4 − 1 d θ = 0 \begin{aligned}
\left| \lim_{R \to \infty} \int_{C_2} \dfrac{dz}{z^4+1} \right| &\leqq \lim_{R \to \infty} \int_{C_2} \dfrac{|dz|}{|z^4+1|}\\
&\leqq \lim_{R \to \infty} \int_0^{\pi} \dfrac{R}{R^4-1} \; d\theta\\
&= 0
\end{aligned} ∣ ∣ R → ∞ lim ∫ C 2 z 4 + 1 d z ∣ ∣ ≦ R → ∞ lim ∫ C 2 ∣ z 4 + 1∣ ∣ d z ∣ ≦ R → ∞ lim ∫ 0 π R 4 − 1 R d θ = 0 lim R → ∞ ∫ C 2 d z z 4 + 1 = 0 \displaystyle \lim_{R \to \infty} \int_{C_2} \dfrac{dz}{z^4+1} = 0 R → ∞ lim ∫ C 2 z 4 + 1 d z = 0 R R R R 4 − 1 > 0 R^4 -1 > 0 R 4 − 1 > 0
以上より
∫ − ∞ ∞ d x x 4 + 1 = lim R → ∞ ∫ C 1 d z z 4 + 1 = lim R → ∞ ∫ C 1 d z z 4 + 1 + ∫ C 2 d z z 4 + 1 = lim R → ∞ ∮ C d z z 4 + 1 = π 2 \begin{aligned}
\int_{-\infty}^{\infty} \dfrac{dx}{x^4+1}
&= \lim_{R \to \infty} \int_{C_1} \dfrac{dz}{z^4+1}\\
&= \lim_{R \to \infty} \int_{C_1} \dfrac{dz}{z^4+1} + \int_{C_2} \dfrac{dz}{z^4+1}\\
&= \lim_{R \to \infty} \oint_{C} \dfrac{dz}{z^4+1}\\
&= \dfrac{\pi}{\sqrt{2}}
\end{aligned} ∫ − ∞ ∞ x 4 + 1 d x = R → ∞ lim ∫ C 1 z 4 + 1 d z = R → ∞ lim ∫ C 1 z 4 + 1 d z + ∫ C 2 z 4 + 1 d z = R → ∞ lim ∮ C z 4 + 1 d z = 2 π
R R R R R R ∮ C f ( z ) d z \displaystyle \oint_C f(z) \; dz ∮ C f ( z ) d z
その他の実積分
様々な実積分を留数定理によって計算できます。他の例は
を参照してください。
 このとき, の での留数 を
と定める。
このとき, の での留数 を
と定める。












