- 分子の次数+1≦分母の次数
- 分母=0 は非負の実数解を持たない
を満たすとき,次のように積分ができます。
無理関数を扱う際の注意点があります。
被積分関数 z21(z2+1)1 は z2+1e−21logz と変形できます。logz の多価性 より {z∣Re(z)>0} に沿って不連続となります。そのため {z∣Re(z)>0} を避けるように積分経路を用意する必要があります。
1番の解答
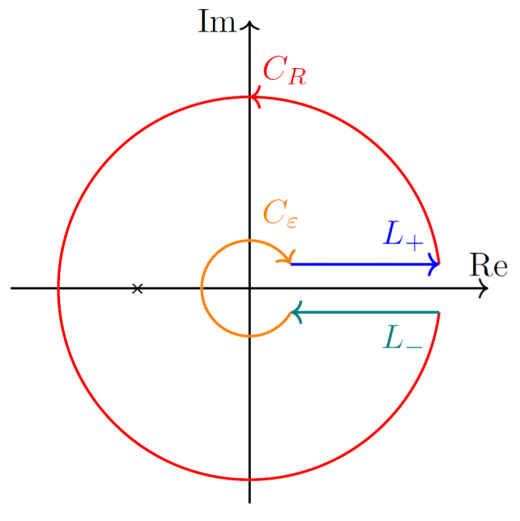
- CR={z∣∣z∣=R,−δ≦Im(z)≦δ}
- Cε={z∣∣z∣=ε,−δ≦Im(z)≦δ}
- L+={z∣Im(z)=δ,ε≦∣z∣≦R}
- L−={z∣Im(z)=−δ,ε≦∣z∣≦R}
と曲線をとり,C を上記の和とする。このとき C は単純閉曲線である。

z21(z2+1)1 の孤立特異点は z=±i であるため,留数定理から
∮Cz21(z2+1)dz=2πi(Res(z21(z2+1)1,i)+Res(z21(z2+1)1,−i))=2πi(z→ilimz21(z+i)1+z→−ilimz21(z−i)1)=πi−21−π(−i)−21=πe−4πi−πe−43πi=22π
である。なお
i−21=(ei2π)−21=e−4πi
と計算した。
CR 上での積分を評価する。
R→∞lim∣∣∫CRz21(z2+1)dz∣∣≦R→∞lim∫CR∣z21∣∣z2+1∣∣dz∣≦R→∞lim∫CR∣z21∣(∣z2∣−1)∣dz∣≦R→∞lim∫02πR21(R2−1)Rdθ=R→∞lim2πR2−1R21=0
である。なお ∣z2∣=∣z2+1+(−1)∣≦∣z2+1∣+∣1∣ より ∣z2+1∣≧∣z2∣−1 であることを用いた。また z から θ に置換したとき,θ での積分の範囲は [0,2π] ではないが,[0,2π] に含まれるため,上記のような不等式で評価してよい。
次に Cε 上での積分を評価する。z2+11 は Cε 上で正則であるため,最大値 M を持つことを用いると
ε→0lim∣∣∫Cεz21(z2+1)dz∣∣≦ε→0lim∫Cε∣z21∣∣z2+1∣∣dz∣≦ε→0lim∫02πε21Mεdθ=ε→0lim2Mπε21=0
L+,L− 上での積分を評価する。
L+ 上で被積分関数は (x+iδ)2+1e−21log(x+iδ) となる。有界区間(今は [ε,R] 上を考える)これは δ→0 で x2+1e−21logx に一様収束する。(後述)
よって
δ→0lim∫L+z21(z2+1)dz=∫εRx2+1e−21logxdx=∫εRx21(x2+1)dx
が得られる。
同様に L− で被積分関数は (x−iδ)2+1e−21log(x−iδ) となり,δ→0 で x2+1e−21(logx+2πi) に一様収束する。なお,logz=log∣z∣+iargz であったことから,L− において argz→2π であることに注意する。
こうして
δ→0lim∫L−z21(z2+1)dz=∫Rεx2+1e−21(logx+2πi)dx=∫Rεx2+1e−21logxe−iπdx=∫Rεx2+1−e−21logxdx=∫εRx2+1e−21logxdx=∫εRx21(x2+1)dx
が得られる。
以上をまとめると
R→∞limε→0limδ→0lim∮Cz21(z2+1)dz=2∫0∞x21(x2+1)dx
となり,R,ε,δ に寄らず
∮Cz21(z2+1)dz=22π
であるため,
∫0∞x21(x2+1)dx=2π
となる。
一様収束の証明
f(z)=z2+1e21logz は一様連続である。
よって任意に正数 ε′ を取ったとき,∣a−b∣<δ′ であれば ∣f(a)−f(b)∣<ε′ とできる。
x∈[ε,R] として
fδ(x)=f(x+iδ)
と定めたとき,δ<δ′ であれば一様連続性から
∣f+0(x)−fδ(x)∣=∣f(x)−f(x+iδ)∣<ε′ である。
よって supx∈[ε,R]∣f+0(x)−fδ(x)∣<ε′ となり一様収束することが従う。
一般的なケース
2番の解答
- CR={z∣∣z∣=R,−δ≦Im(z)≦δ}
- Cε={z∣∣z∣=ε,−δ≦Im(z)≦δ}
- L+={z∣Im(z)=δ,ε≦∣z∣≦R}
- L−={z∣Im(z)=−δ,ε≦∣z∣≦R}
と曲線をとり,C を上記の和とする。このとき C は単純閉曲線である。
za(z+1)1 の孤立特異点は z=−i であるため,留数定理から
∮Cza(z+1)dz=2πiRes(za(z+1)1,−1)=2πiz→−1limza1=2πiz→−1lime−alogx=2πie−aiπ
である。
CR 上での積分を評価する。
R→∞lim∣∣∫CRza(z+1)dz∣∣≦R→∞lim∫CR∣za∣∣z+1∣∣dz∣≦R→∞lim∫CR∣za∣(∣z∣−1)∣dz∣≦R→∞lim∫02πRa(R−1)Rdθ=R→∞lim2πR−1R1−a=0
である。なお z から θ に置換したとき,θ での積分の範囲は [0,2π] ではないが,[0,2π] に含まれるため,上記のような不等式で評価してよい。
次に Cε 上での積分を評価する。z+11 は Cε 上で正則であるため,最大値 M を持つことを用いると
ε→0lim∣∣∫Cεza(z+1)dz∣∣≦ε→0lim∫Cε∣za∣∣z+1∣∣dz∣≦ε→0lim∫02πεaMεdθ=ε→0lim2Mπε1−a=0
である。
L+,L− 上での積分を評価する。
L+ 上で被積分関数は (x+iδ)+1e−alog(x+iδ) となる。有界区間(今は [ε,R] 上を考える)これは δ→0 で x+1e−alogx に一様収束する。
よって
δ→0lim∫L+za(z+1)dz=∫εRx+1e−alogxdx=∫εRxa(x2+1)dx
が得られる。
同様に L− で被積分関数は (x−iδ)+1e−alog(x−iδ) となり,δ→0 で x+1e−a(logx+2πi) に一様収束する。なお,logz=log∣z∣+iargz であったことから,L− において argz→2π であることに注意する。
こうして
δ→0lim∫L−za(z+1)dz=∫Rεx+1e−a(logx+2πi)dx=∫Rεx+1e−alogxe−2aiπdx=∫Rεx+1e−2aiπe−alogxdx=∫εRx+1−e−2aiπe−alogxdx=∫εRxa(x+1)−e−2aiπdx
が得られる。
以上をまとめると
R→∞limε→0limδ→0lim∮Cza(z+1)dz=(1−e−2aiπ)∫0∞xa(x+1)dx
となり,R,ε,δ に寄らず
∮Cza(z+1)dz=1−e−2aiπ2πie−aiπ=eaiπ−e−aiπ2iπ=sinπaπ
であるため,
∫0∞xa(x2+1)dx=sinπaπ
となる。
0<a<1,b>0 のとき,同様にして
∫0∞xa(x2+b2)dx=2b1+acos2aππ
と計算されます。
類題(京都大学院数学・数理科学専攻 2019)
a は 0<a<1 を満たす定数とする。このとき広義積分
∫0∞1+x2xadx
を求めよ。














