有理式を R(z)=P(z)/Q(z) と表したとき
- degP+1≦degQ
- Q(z)=0 の実数解は重解ではない
を満たすときは次のように積分をしましょう。
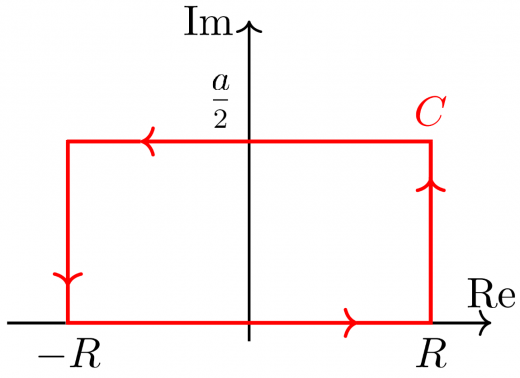
- 次のように閉曲線を取る
- 実部が正の特異点をすべて含むように,十分大きな R を半径とする半円を取る
- 実軸上の特異点の周囲 ε を避けるように −R から R へ直線を取る
- 特異点周りには(上で取った直線とつながるように)小さな半円を取る
- 閉曲線周りの積分値を留数定理から求める
- R→∞,ε→0 の評価をする
計算では,オイラーの公式により eiz の積分をすることを考えます。
解
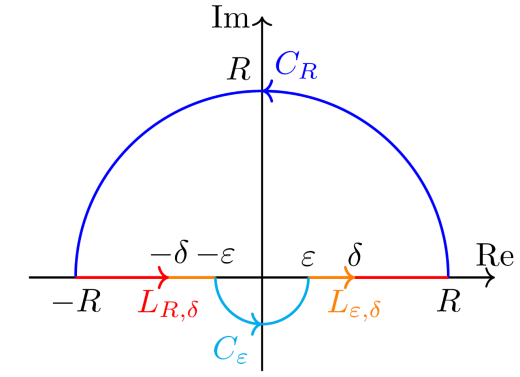
十分小さい δ>0 を取る。R を δ より大になるように取る。
- CR={z∈C∣∣z∣=R,Imz≧0}(下図青色)
- LR,δ:実軸上の区間 [−R,−δ] と [δ,R] の和(下図赤色)
- Lε,δ:実軸上の区間 [−δ,−ε] と [ε,δ] の和(下図橙色)
- Cε={z∈C∣∣z∣=ε,Imz≦0}(下図水色)
と定め,C を上記4曲線の和とする。このとき C は単純閉曲線である。
オイラーの公式より
zeiz=zcosz+izsinz
である。zeiz を C で積分して,その虚部を調べればよい。
zeiz の孤立特異点は z=0 で位数は1であるため,留数定理から
∮Czeizdz=2πiRes(zeiz,0)=2πiz→0limeiz=2πi
である。
CR での積分を評価する。
R→∞lim∣∣∫CRzeizdz∣∣≦R→∞lim∫CR∣∣zeizdz∣∣=R→∞lim∫0π∣∣ReiθeiReiθiReiθ∣∣dθ=R→∞lim∣∣eiRcosθe−Rsinθ∣∣dθ=R→∞lim∫0πe−Rsinθdθ
と計算される。
最後の積分を詳しく評価する。下図に示す通り 0≦θ≦2π で sinθ≧π2θ である。
これを用いて式を変形すると
∫0πe−Rsinθdθ=2∫02πe−Rsinθdθ≦2∫02πe−Rπ2θdθ=Rπ−Rπe−R→0(R→∞)
であるため,
R→∞lim∫CRzeizdz=0
である。
ε→0 のときの Cε
上の積分を評価する。zeiz は z=0 で1位の極を持つ。ゆえに正則関数 h(z) を用いると,z=0 近傍で zeiz をローラン展開したものを zc−1+h(z) と表すことができる。h(z)
は正則であるため ∣h(z)∣ は Cε 上で最大値を取る。
こうして
ε→0lim∣∣∫Cεh(z)dz∣∣≦ε→0lim∫Cε∣h(z)∣dz=ε→0limπεz∈Cεmax(∣h(z)∣)=0
である。一方
∫Cεzc−1dz=∫π2πεeiθc−1εieiθdθ=πic−1=πiRes(zeiz,0)=πiz→0limzzeiz=πi
である。よって
ε→0lim∫Cεzeizdz=πi
LR,δ,Lε,δ での積分は,LR,δ は εに,Lε,δ は R に寄らないことから各々の極限を考えれば良く,
R→∞limε→0lim∫LR,δ+Lε,δzeizdz=R→∞lim∫LR,δzeizdz+ε→0lim∫Lε,δzeizdz=p.v.∫−∞∞xeixdx
となる。
なお p.v.∫ に関しては,後述する主値積分を参照してください。広義積分の一種と考えて問題ありません。
以上をまとめると
R→∞limε→0lim∮Czeizdz=R→∞limε→0lim∫LR,δ+Lε,δzeizdz+R→∞lim∫CRzeizdz+ε→0lim∫Cεzeizdz=p.v.∫−∞∞xeixdx+πi
及び
R→∞limε→0lim∮Czeizdz=2πi
であるため,
p.v.∫−∞∞xeixdx=πi
である。
p.v.∫−∞∞xeixdx=p.v.∫−∞∞xcosxdx+p.v.∫−∞∞ixsinxdx
より,実部と虚部を比較して
∫0∞xsinxdx=21p.v.∫−∞∞xsinxdx=2π
を得る。
有理式の仮定がどのように効いているかを確認します。
CR 上の積分の評価のとき,有理式の次数と eiz を被積分関数に含むことが効いて,R→0 で積分が 0 に収束することがわかります。
また Q(z) が重解を持たない仮定により Cε 上の積分の評価で見通しよく計算できます。
sinc 関数
zsinz は
sinc 関数(シンク関数) と呼ばれ,信号処理などの分野で非常に重要な関数となります。
sinc 関数は z=0 を孤立特異点に持ちますが,この特異点は可除特異点になるので z=0 でも正則であるとみなすことができます。よって本質的には,sinc 関数の実数全体の積分は主値積分と扱わなくても良いです。
一方 zeiz は z=0 で極を持つので主値積分として考える必要があります。
発展例題
応用例題
次の積分を求めよ。
∫−∞∞(xsinx)3dx
三倍角の公式を使えば z3sinz の形に帰着できます。
しかし下手をすると Cε での評価が難しくなるかもしれません。
証明
三倍角の公式により sin3x=43sinx−sin3x であるため
∫−∞∞4z33eiz−e3izdz
を計算すればよい。
積分路を前の問題3と同じように取ると,同様の議論から
R→∞lim∫CR4z33eiz−e3izdz=0
であるため
∫−∞∞(xsinx)3dx=−ε→0lim∫Cε4z33eiz−e3izdz
を得る。
一方 z=0 近傍でローラン展開すると,被積分関数は
2z31+4z3+i−1613z+⋯
である。0 次以上の項は前の例題同様 ε→0 で消える。
−3 次の項は
∫Cεz3dz=∫−π0ε−2ie−2iθdθ=[−2ε2e−2iθ]−π0=0
となり消える。
こうして
ε→0lim∫Cε4z33eiz−e3izdz=−43πi
であるため
∫−∞∞(xsinx)3dx=43π
となる。
∫−∞∞x3sin3xdx=27∫−∞∞x3sinxdx
であることから x3sinx の積分だけを計算すればいいと考えてしまうと,Cε で積分が消えません。
実はわざわざ分けない方が上手くいくという計算例でした。
また,わざわざ三倍角の公式を使わなくとも,そのままの形からローラン展開を用いて計算することもできます。