ディリクレ関数の定義と有名な3つの性質
更新
実数全体で定義され,有理数のときに ,無理数のときに を取る関数をディリクレ関数と言う。
ディリクレ関数について,以下の話題を解説します。
- いたるところで不連続
- と極限で表せる
- リーマン積分不可能,ルベーグ積分可能(高校範囲外)
連続性
連続性
ディリクレ関数はいたるところで不連続である。
これは以下の2つの事実から分かります。
- 有理数 を一つ固定すると, にいくらでも近い無理数を取ってこれる
- 無理数 を一つ固定すると, にいくらでも近い有理数を取ってこれる
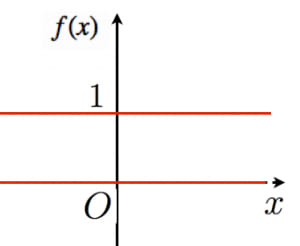
ディリクレ関数は「任意の点で関数のグラフがつながっていない」という不思議な関数です。グラフを強引に描こうとすると図のようになります。点同士が重なり合って線みたいに見えます。
cosと極限で表せる
cosと極限で表せる
ディリクレ関数 は以下のように表せる:
かなりかっこいい式です!
中括弧の中は と のみに依存することに注意して,
とおく。
-
が有理数のとき
が十分大きければ は整数,つまり
よって, が十分大きいとき
つまり, -
が無理数のとき
任意の に対して は整数でない,つまり
よって,任意の に対して
つまり,
リーマン積分とルベーグ積分
リーマン積分とルベーグ積分
ディリクレ関数の積分
ディリクレ関数の積分
ディリクレ関数 の区間 上での積分を考えてみます。大雑把な説明です。
縦にいくら細かく切っても,長方形の縦の長さを にしてよいか にしてよいのかが決まらない(上リーマン和と下リーマン和の極限が一致しない)。
よって,ディリクレ関数は 上でリーマン積分不可能。
区間において,
を与える たち(無理数の集合)が占める区間の「大きさ」(ルベーグ測度)は である(注)。
を与える たち(有理数の集合)が占める区間の「大きさ」は である。
よって,ルベーグ積分の値は である。
(注)直感的には 区間内の実数のほとんどが無理数であることから。厳密には測度の完全加法性より可算集合のルベーグ測度が であることから(有理数は可算無限集合)。→集合の濃度と可算無限・非可算無限
このようなヤバい関数が楽しい!という人もいますし,ヤバい関数は実際出てこないから都合のいい関数だけ考える,という人もいます。











