ルベーグ測度

$\mathbb{R}$ における区間と体積

$a,b \in \mathbb{R} \cup \{ \pm \infty \}$（$a < b$）によって $$(a,b] = \{ x \mid a < x \leqq b \}$$ と表される集合 $I$ を（$\mathbb{R}$ 内の）区間 といいます（$(a,\infty]$ は $(a,\infty) = \{ x \mid a < x \}$ と考えます）。ただし，空集合 $\emptyset$ も区間とみなします。

区間の体積 $\mathrm{vol} \ (I)$ を $$\mathrm{vol} \ (I) = b-a$$ と定義します。ただし，$\infty - a$，$b- (-\infty)$，$\infty - (-\infty)$ は $\infty$ とします。

有限個の互いに素な区間 $I_1 , I_2 , \cdots , I_n$ を用いて $$E = I_1 \cup I_2 \cup \cdots \cup I_n$$ と表される集合を区間塊といいます。区間塊全体の集合を $\mathfrak{F}$ とおきます。

$E \in \mathfrak{F}$ の体積を $$\mathrm{vol} \ (E) = \sum_{i=1}^n \mathrm{vol} \ (I_i)$$ と定義します。

※ 文献によっては $(a,b]$ ではなく $[a,b)$ とすることもあります。

$\mathbb{R}^n$ における区間と体積

区間の概念を $n$ 次元に拡張します。

$a_1, \cdots , a_n$，$b_1 , \cdots , b_n \in \mathbb{R} \cup \{ \pm \infty \}$（各 $i$ で $a_i < b_i$）を用いて $$\begin{aligned} &\prod_{i=1}^n (a_i,b_i]\\ &= (a_1,b_1] \times (a_2,b_2] \times \cdots \times (a_n,b_n]\\ &= \{ (x_1 , \cdots , x_n) \mid \text{各} \ i \ \text{で} \ a_i < x_i \leqq b_i \} \end{aligned}$$ と表される集合 $I$ を（$\mathbb{R}^n$ 内の）区間 といいます。（ここでも $(a_i,\infty) = \{ x_i \mid a_i < x_i \}$ と考えます。）

2次元では長方形，3次元では直方体になります。

区間の体積を $$\mathrm{vol} \ (I) = (b_1 - a_1) (b_2 - a_2) \cdots (b_n - a_n)$$ と定義します。

区間塊とその体積も $\mathbb{R}$ のときと同様に定義します。

例

• $I = (1,2]$ のとき $\mathrm{vol}\ (I) = 2-1 =1$ です。
• $I = (1,2] \times (3,5]$ のとき $\mathrm{vol}\ I = (2-1)(5-3)=2$ です。

区間塊と体積の性質

$\mathbb{R}^n$ における区間塊全体の集合 $\mathfrak{F}$ には次の性質があります。

性質1～3を満たす部分集合族を有限加法族と言います。

また，体積には次の性質があります。

※ なお，性質1～3を満たす関数を有限加法的測度と言います。さらに性質4も満たす関数を完全加法的測度と言います。$\mathrm{vol}$ は完全加法的測度です。

証明にも挑戦してみてください。

以下 $\mathbb{R}^n$ で考えます。

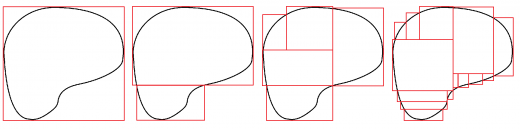
区間塊ではない集合 $A\subseteq\mathbb{R}^n$ に対して体積を定義しましょう。

やり方は簡単で「集合を区間塊に近似」して測ります：

$$\mu^* (A) := \inf_{A \subset \bigcup E_i\\ E_i は区間} \sum_{i=1}^{\infty} \mathrm{vol} \ (E_i)$$

$A$ を含むいろいろな区間塊の中で，体積のinfを取っています。

これをルベーグ外測度といいます。

性質

1，2 は定義からすぐにわかります。3 は少々難しいです。

いくつかの例

区間塊

区間塊に対しては $\mu^* (E) = \mathrm{vol}\ (E)$ です。

開区間・閉区間

開区間 $(a,b)$，閉区間 $[a,b]$ では $\mu^* ((a,b)) = \mu^* ([a,b]) = b-a$ です。

$b-a > \varepsilon$ となる正の実数 $\varepsilon$ を取ると，$(a , b - \varepsilon] \subset (a,b) \subset (a,b]$ なので $b-a-\varepsilon < \mu^{\ast} ((a,b)) < b-a$ となります。$\varepsilon \to 0$ とすることで $\mu^{\ast} ((a,b)) = b-a$ を得ます。

1点集合

1点集合 $\{ p \}$（$p \in \mathbb{R}$）で外測度を計算してみましょう。

任意の正整数 $n$ に対して $I_n = \left( p-\dfrac{1}{n} , p + \dfrac{1}{n} \right]$ は，$p$ を含みます。$\mathrm{vol}\ (I_n) = \dfrac{2}{n}$ であるため，$n$ を大きく取ると，$\mathrm{vol}\ (I_n)$ はいくらでも $0$ に近付きます。そのため $\mu^* (\{ p \}) = 0$ です。

今回は $\mathbb{R}$ で考えましたが，$\mathbb{R}^n$ でも同様です。

平行移動

$A \subset \mathbb{R}^n$ に対して $-A = \{ -a \mid a \in A \}$，$A+x = \{ a+x \mid a \in A \}$ とおくと，$\mu^* (A) = \mu^* (-A) = \mu^* (A+x)$ です。

問題

$\mu^*$ は完全加法性を満たすのでしょうか。

つまり，$\{ X_i \}$ を $\mathbb{R}^n$ の部分集合族で，$i \neq j$ のとき $X_i \cap X_j = \emptyset$ としたとき， $$\mu^* \left( \bigcup_{i=1}^{\infty} X_i \right) = \sum_{i=1}^{\infty} \mu^* (X_i)$$ となるのでしょうか。

実は「No」です。

というわけで，完全加法性を妨げる奇妙な集合は取り除いてしまいましょう。

次に紹介するルベーグ可測集合は「奇妙ではない」集合のカテゴライズです。

ルベーグ可測集合

• ルベーグ可測集合全体の集合を $\mathfrak{M}$ と書きます。
• 上記の条件をカラテオドリの条件といいます。

ルベーグ可測集合の定義は一見分かりにくいですが，この定義から以下の便利な性質が得られます。

※以下，ルベーグ可測のことを単に「可測」と書く場合があります。

1 は定義より明らかです。2～4 は少々難しいです。測度・ルベーグ積分の本を参照してください。

完全加法族

$\Sigma$ を $X$ の空でない部分集合族とします。

1. $E \in \Sigma \Longrightarrow E^c \in \Sigma$ となる。
2. $\{ E_i \}$ を $E_i \in \Sigma$ となる可算な集合族とすると，$\displaystyle \bigcup_{i=1}^{\infty} E_i \in \Sigma$ となる。

この2条件を満たす $\Sigma$ を完全加法族もしくは $\boldsymbol{\sigma}$ 加法族といいます。ルベーグ可測集合の全体 $\mathfrak{M}$ は完全加法族です。

完全加法族は今回これ以上掘り下げませんが，一般の集合に測度を導入する際に活躍します。

ルベーグ測度

ルベーグ測度は，ルベーグ外測度の性質に加えて，次の性質を持ちます。

具体例

簡単な例

区間塊は可測集合です。よって，区間塊 $E$ に対して $\mu (E) = \mathrm{vol}\ (E)$ である。

1点集合は可測です。

可算な集合は1点集合が可算個集まったものです。そのため可算集合は可測です。さらに測度の完全加法性より，可算集合の測度は $0$ です。

一般に次の命題が成り立ちます。

開集合と閉集合

開集合と閉集合はルベーグ可測集合です。テクニカルな方法で証明します。集合論に自信がある方はぜひチャレンジしてください。

実は測度は開集合によって「近似」できます。

ポイントは，可測集合ではないものも近似ができることです。非常に有用なので計算でしばしば使います。

カントール集合

カントール集合 とは，区間 $[0,1]$ から「線分を三等分して真ん中を取り除く」という操作を無限回繰り返して得られる集合でした。

カントール集合 $X$ の外測度を計算してみましょう。

$X_n$ で $n$ 回目の操作までに取り除かれた区間とします。このとき $\displaystyle X = \bigcap_{i=1}^{\infty} X_i$ です。 $\mu^* ([0,1]) = \mu^* (X) + \mu^* ([0,1] \backslash X)$ なので，$[0,1] \backslash X_n$ を計算していきましょう。 $$\mu^* ([0,1] \backslash X_n) = \dfrac{1}{3} + \dfrac{1}{3} \dfrac{2}{3} + \cdots + \dfrac{1}{3} \left( \dfrac{2}{3} \right)^n$$ であるため， $$\begin{aligned} \mu^* ([0,1] \backslash X) &= \dfrac{1}{3} \left\{ 1 + \dfrac{2}{3} + \left( \dfrac{2}{3} \right)^2 + \cdots \right\}\\ &= 1 \end{aligned}$$ となります。よって $$\mu^* (X) = \mu^* ([0,1]) - \mu^* ([0,1] \backslash X) = 0$$ です。

このように非可算な集合でも外測度は $0$ になり得ます。

こうしてカントール集合は可測集合となります。

奇妙な例

特殊な同値関係を考えます。$x,y \in (0,1]$ に対して $$x \sim y \Longrightarrow x- y \in \mathbb{Q}$$ により同値関係を定めます。この商集合 $(0,1] / \sim$ の代表元の集合を $X$ とおきます。

$X$ がルベーグ可測集合と仮定しましょう。

$\mathbb{Q} \cap [0,1] = \{ p_1 , p_2, \cdots \}$ とおきましょう。

$$X_n = \{ \{ x + p_n \} \mid x \in X \}$$ （ただし $\{ x \}$ で $x$ の小数部分を表すこととします。）

$i \neq j$ のとき $X_i \cap X_j = \emptyset$ です。実際，$X_i \cap X_j \neq \emptyset$ を仮定すると $\{ x + p_i \} = \{ x' + p_j \}$（$x,x' \in X$）とできます。$x-x' \in \mathbb{Q}$ ですが，$X$ の定義より $x - x' \notin \mathbb{Q}$ となり矛盾します。

$$(0,1] = \bigcup_{n=1}^{\infty} X_n$$ となるため， $$1 = \mu ((0,1]) = \sum_{n=1}^{\infty} \mu (X_n)$$ です。

$\mu (X) = \mu (X_n)$ であるため， $$1 = \sum_{n=1}^{\infty} \mu (X) \quad \cdots\cdots (\ast)$$ です。

$\mu (X) \neq 0$ のとき，$(\ast)$ の右辺は $\infty$ に発散します。一方 $\mu (X) = 0$ のとき，$(\ast)$ の右辺は $0$ となります。

結果，$\mu (X)$ の値がどうであれ，$(\ast)$ の式は成り立ちません。

以上の議論から $X$ は可測ではありません。

この $X$ は ヴィタリ集合 と言われています。

$\mathbb{R}^n$ の部分集合 $A$ に一般的な「体積」を定義できました。具体的には2つの方法で計算します。

1. $A$ を区間で覆い近似する。
2. $A$ を開集合で近似する。

測度が $0$ の集合をうまく使うことでバナッハ=タルスキのパラドックスという非常に面白い定理が証明できます。こちらはまた次の機会にしましょう。

測度の概念からルベーグ積分を定義できます。ルベーグ積分の世界で考えと，項別積分といった「極限と積分の入れ替え」についての議論を精密に行うことができるようになります。次回以降の記事をお楽しみに。