多変数関数の極値判定とヘッセ行列
更新
多変数関数(特に二変数関数)の極値判定法とヘッセ行列について解説します。
ヘッセ行列を使うと,多変数関数が極値を取るための必要条件,極大点・極小点であるための十分条件がわかります。
まずは結論です:
多変数関数 が点 において,(偏微分がすべて )を満たし,さらに,
- での のヘッセ行列が正定値である場合,極小値をとる。
- での のヘッセ行列が負定値である場合,極大値をとる。
級二変数関数 が点 において, を満たすとする。
とおいたとき,
- , のとき極小
- , のとき極大
- のとき極値をもたない
この記事の目標は,上記の意味を理解することです。
準備は大変なので 具体例 から読んでもいいでしょう。
ヘッセ行列と行列の正定値性
ヘッセ行列と行列の正定値性
ヘッセ行列
ヘッセ行列(二階の偏導関数を並べた行列)について説明します。以下,この記事で関数 は 級(二階連続微分可能)とします。
変数関数 に対して,
成分が であるような 行列をヘッセ行列と言う。
のヘッセ行列を求めよ。
を で偏微分すると,
で偏微分すると,
これらを用いて二階の偏導関数を求める:
よってヘッセ行列は
注: が 級のとき偏微分の順序は交換できるのでヘッセ行列は必ず対称行列になります。
なお,ヘッセ行列の行列式のことをヘッシアンと言うことがあります。
正定値,負定値とは
実対称行列 に対して以下の条件は全て同値である。このいずれか(したがって全て)を満たす行列を正定値行列と言う。
-
全ての( ベクトルではない) 次元縦ベクトル に対して が正
-
の固有値が全て正
-
首座小行列(左上の 行列 )の行列式が全て正。
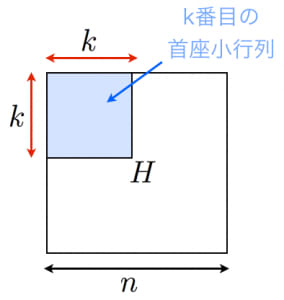
が正定値のとき を負定値と言います。
行列のサイズが小さいときに正定値かどうかの判定をしたいときは3を使うのが楽です(固有値の計算はけっこう大変なので2は使いづらいです)。
極値
極値
臨界点(停留点)
極値の定義の前に,極値の候補になり得る臨界点(停留点)を定義します。
臨界点とは「傾きが (すべての偏微分係数が )」の点です。
多変数関数 が において を満たすとき, を臨界点(停留点)という。
極値の定義
極値判定をする前に極値の定義をしっかりと確認しましょう。
多変数関数 が において
- 極大である とは, と十分近い任意の点 に対して となることを表す。
- 極小である とは, と十分近い任意の点 に対して となることを表す。
一旦,二変数で表すと
-
十分近いを数式で表現するときは,十分小さい について や などと表現すると良いでしょう。
-
文献によっては,極大の定義 に等号を含めず とすることもあります。極小も同様です。
極値であれば停留点になります。よって極値を探す場合,まず停留点から探すことになります。
極値ではない停留点
停留点であっても極値を取らない場合があります。
直線・曲線を成すとき

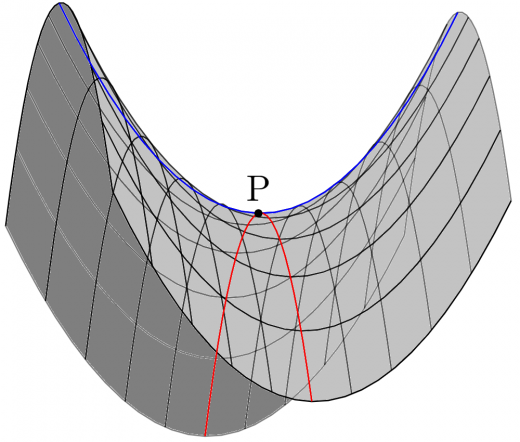
鞍点
下のように,ある方向から見ると極小・ある方向から見ると極大になっている点を鞍点(サドルポイント)といいます。
極値判定の定理
極値判定の定理
一変数関数の場合,以下が成立しました。
-
極値の必要条件: が で極大または極小→
-
極小の十分条件: かつ → で極小
-
極大の十分条件: かつ → で極大
これの多変数版は以下のようになります:
-
極大または極小→その点で偏導関数の値が全て0
-
その点で偏導関数の値が全て0かつ ヘッセ行列が正定値 → 極小
-
その点で偏導関数の値が全て0かつ ヘッセ行列が負定値 → 極大
さらに,
- その点で偏導関数の値が全て0かつ ヘッセ行列の固有値が正のものと負のものがある → 鞍点
なお,ヘッセ行列が上記のどれでもないとき,つまりヘッセ行列の行列式が 0 である(固有値に 0 がある) 場合は力技で極小か極大か,それともどちらでもないかを調べることになります。
固有値に 0 がある例
とします。
, です。 が極大・極小をとる点の候補です。
でのヘッセ行列は です。判定法からは極大・極小はわかりません。
は下図のようになります。 は,赤い曲線方向で見ると定数ですが,(等号を含めた定義では)極小です。

二変数の極値判定
二変数の極値判定
二変数関数である場合は簡単に判定をすることができます。
級二変数関数 が点 において, を満たすとする。
とおいたとき,
- , のとき極小
- , のとき極大
- のとき極値をもたない
このようにヘッセ行列を計算しなくとも判別ができます。
しかし本質的にはヘッセ行列の首座行列式を計算していることと何ら変わりありません。
行列の首座小行列は 成分と元の行列の2つである。
ヘッセ行列の場合, と元のヘッセ行列 の2つである。
またヘッセ行列は であるため,行列式は である。(今回 級を考えているため である)
- 極小
このとき,ヘッセ行列は正定値である。これは首座行列式がすべて正であることと同値であった。
首座行列式は と であるため,定理が従う。
- 極大
このとき,ヘッセ行列は負定値である。 の首座行列式がすべて正であることと同値であった。
このとき正である値は と であるため,定理が従う。
※ 行列の場合, である。(定義より分かる)
- 鞍点
固有値が正負両方である場合である。今回は 行列であるため,固有値は2つである。
よって,鞍点である場合とヘッセ行列の行列式が負であることが同値である。
具体例
具体例
実際に二変数関数の極値を求めてみます。
例題
の極値をできる限り求めよ。
極値の候補
まず,極値のための必要条件として偏微分=0を解く:
より
つまり極値の候補は二つ。
今後の計算のため,二階微分も計算しておく。
の判定
いくつかの方法で解いてみましょう。
ヘッセ行列は では
これは以下のように正定値であることが分かる:
一つ目の首座小行列式( 成分の値)は
二つ目の首座小行列式は
よって, は極小点であり極小値は である。
より極小値を取る。
の判定
ヘッセ行列は では
固有値を計算する。 より固有値は で正負どちらにもなる。
よって鞍点を取る。
より鞍点を取る。
ある方向からは極大・ある方向からは極小であることを具体的に計算してみます。
平面 上で は となる。これは で極大値を取る。
一方,平面 上で は となる。これは で極小値を取る。
よって は で鞍点になる。
正定値・負定値の補足
正定値・負定値の補足
の首座小行列式はそれぞれ , であるから,この行列は負定値なのでは?
よくあるミスです。
が負定値であるとは, が正定値であるという定義でした。
の首座小行列式は,それぞれ , です。
よってこの行列は正定値でも負定値でもありません。
判別式を用いた説明もときどき見かけますが,二変数関数のときにしか通用しないので私はあまり好きではありません。











