sup（上限）とinfの意味，maxとの違い

更新日時 2021/03/07

要素が実数である集合 AA に対して

  • max⁡A\max A：AA の最大値，maximum(英語)，マックス(読み方の例)

  • min⁡A\min A：AA の最小値，minimum，ミン

  • sup⁡A\sup A：AA の上限，supremum，スープ

  • inf⁡A\inf A：AA の下限，infimum，インフ

大学数学（解析）で学ぶ sup⁡\sup の意味について解説します。

min⁡\min は max⁡\max の反対側，inf⁡\inf は sup⁡\sup の反対側なので，ここでは max⁡,sup⁡\max,\sup についてのみ解説します。

目次

  • maxとsupの定義

  • 具体例

  • supはmaxの一般化

  • supは常に存在する

maxとsupの定義

まずは集合の最大値 max⁡\max の定義です。

max⁡A=c  ⟺  \max A=c\iff

  • 任意の x∈Ax\in A に対して x≤cx\leq c かつ
  • c∈Ac\in A

1つめの条件は，「cc はどの要素よりも小さくはない」つまり「cc は AA の上界」であることを表しています。

次に集合の上限 sup⁡\sup の定義です。

sup⁡A=c  ⟺  \sup A=c\iff

  • 任意の x∈Ax\in A に対して x≤cx\leq c かつ
  • cc より小さい任意の実数 rr に対して，r<xr <x なる x∈Ax\in A が存在する（少しでも小さくすると上界でなくなる）

supの1つめの条件は，maxの1つめの条件と同じです。supの意味は「上界の最小値」です。

具体例

例1

閉集合 A=[a,b]A=[a,b] に対して，max⁡A=b\max A=b，sup⁡A=b\sup A=b

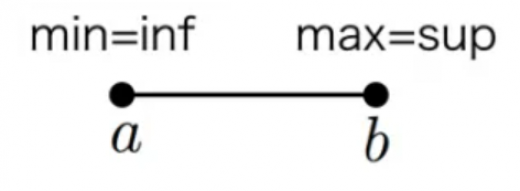
supとinfの具体例

AA の最大値も上限も bb です。

例2

開集合 A=(a,b)A=(a,b) に対して，max⁡A\max A は存在しない，sup⁡A=b\sup A=b

supとinfの具体例

最大値は存在しませんが，上限は存在します。

max⁡\max と sup⁡\sup の定義をもとに，例1と例2を確認してみてください！

supはmaxの一般化

ここからは sup⁡\sup の有用性をなんとなく実感してもらうために，sup⁡\sup の性質を2つ解説します。

sup の嬉しさ1

max⁡A\max A が存在するなら sup⁡A=max⁡A\sup A=\max A

sup⁡\sup は max⁡\max を拡張した概念になっているというわけです！

ほぼ自明ですが一応証明しておきます。

証明

max⁡A=c\max A=c のとき，max⁡\max の定義より，

  1. 任意の x∈Ax\in A に対して x≤cx\leq c

  2. c∈Ac\in A

sup⁡A=c\sup A=c を証明したいが，sup⁡A=c\sup A=c の条件の一つめは1そのものであり成立。二つ目は x=cx=c とすれば，2より成立。

supは常に存在する

sup の嬉しさ2

AA が空でなく，上に有界なら sup⁡A\sup A は常に存在する。

max⁡\max は存在するとは限りませんが，sup⁡\sup は(空でない場合は)常に存在するので，統一的に議論することができます。 sup⁡\sup の存在証明は解析学の教科書を参照して下さい（例えば高木貞治の解析概論）。

supが存在する条件として「AA が空でない」が必要でした。ご指摘いただいた読者の方，ありがとうございます！

この記事の編集者
マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！