いろんな関数 に関する57記事をまとめました。くわしくは各リンク先を見てください。
グラフの平行移動の公式
関数 y=f(x) のグラフを
x
軸方向に
a,y
軸方向に
b
平行移動したグラフを表す式は
y−b=f(x−a)
つまり,x を x−a に変えて,y を y−b に変えればよい。
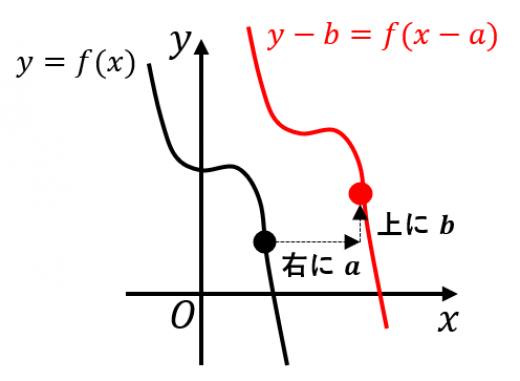
→グラフの平行移動(具体例と公式の証明)
関数のグラフの拡大の公式
y=f(x) のグラフを,原点中心に x 軸方向に A 倍,y 軸方向に B 倍すると,x を Ax に変えて y を By に変えた以下の関数になる:
By=f(Ax)
→関数のグラフの拡大・縮小の証明と例
この記事では,y=cx+dax+b という一次分数関数について説明します。分数関数の基本形とグラフの描き方を説明します。
→一次分数関数のグラフと漸近線
f(x) が偶関数のとき,∫−aaf(x)dx=2∫0af(x)dx
f(x) が奇関数のとき,∫−aaf(x)dx=0
→偶関数と奇関数の意味,性質などまとめ
二次関数のグラフの軸と頂点
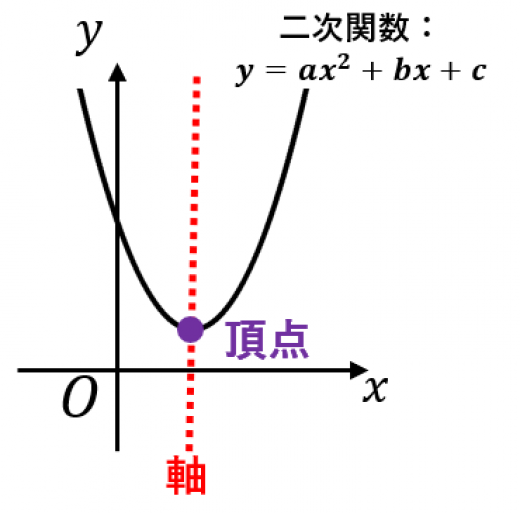
→二次関数のグラフの軸と頂点の求め方など
無理関数
y=±ax+b+c
のグラフは
(−ab,c)
から(定義域,値域を見て)適切な向きに,最初は一瞬鉛直な方向に進んで徐々に変化がなだらかになるように書けばよい。
→無理関数とそのグラフの書き方
微分可能な関数
y=f(x)
上の点
A(a,f(a))
における接線の方程式は,
y−f(a)=f′(a)(x−a)
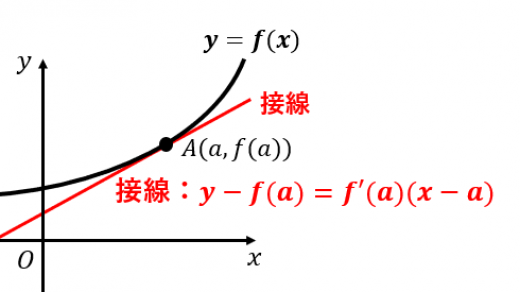
→微分を用いた接線の方程式の公式
二次関数の最大値の求め方
二次関数 y=ax2+bx+c の最大値・最小値は,以下の2通りの方法で求めることができる:
- 平方完成→グラフを描く→最大値,最小値を求める
- 微分する→最大値,最小値を求める
→二次関数の最大値,最小値の2通りの求め方
合成関数の定義
2つの関数 f(x),g(x) に対して,f(g(x)) のことを,f(x) と g(x) の合成関数と言い,f∘g または (f∘g)(x) と書く。
→合成関数について理解しておくべき性質まとめ
- 平方完成による解法(定番)
- 偏微分を用いる解法(計算が一番楽)
- 判別式を用いる解法(考え方が重要)
→二変数の二次関数
三次関数のグラフの対称性

三次関数のグラフに関して以下の性質が成り立つ:
-
変曲点に関して点対称である
-
図において,A,B,C,D,E
は等間隔に並んでいる(4等分の法則)
(C
は変曲点,B,D
は極大,極小点,A,E
は極大,極小点と同じ高さの点の
x
軸への射影)
→三次関数の対称性と4等分の法則
ポイント
このように,通る3点が与えられる二次関数の決定問題は,
二次関数を y=ax2+bx+c とおいて,a,b,c を計算する
という方法で解けます。
→二次関数の決定とその背景
1/3公式
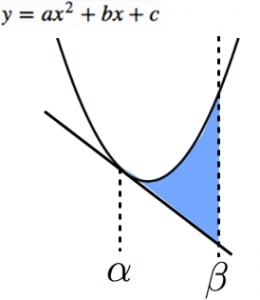
- 放物線 y=ax2+bx+c
- 放物線と x=α で接する接線
- x=β
という3つのグラフで囲まれた部分の面積は,
3∣a∣∣β−α∣3
→1/3公式と1/12公式の意味と証明【二次関数・三次関数と面積】
一次不等式で表される領域内で一次関数の値を最大化(または最小化)する問題を線形計画法(Linear Programming, LP)と言う。
→領域における最大・最小問題(線形計画法)
四次関数
y=ax4+bx3+cx2+dx+e
のグラフの概形
特徴1.上から入ってきて上に抜けていく
特徴2.極小点(コブ)は一つか二つ
→四次関数のグラフの概形と例題2問
陽関数と陰関数の定義
x の値を決めたら y の値が1つに決まるとき,y は x の関数であるという。その中でも,
-
陽関数とは,y=f(x)
という「いつもの形」で表された関数のこと。
-
陰関数とは,F(x,y)=0
という形で表された関数のこと。
→陰関数と陽関数の意味と違いについて
y=∣x−3∣ など,絶対値を含む関数のグラフは,以下の3通りの方法で描けます。
- 中身の符号で場合分けして絶対値を外す方法
- 負の部分を折り返す方法
- maxと見る方法
→絶対値を含む関数のグラフの3通りの書き方
変曲点の意味
変曲点には「グラフの曲がり方が変わる点」という意味がある。
→変曲点の意味といろいろな例
x→+0limxlogx=0
→xlogxの極限,グラフ,積分など
単調増加の定義
関数 y=f(x) と区間 I について,
-
任意の x1,x2∈I に対して,x1<x2 ならば f(x1)≤f(x2) を満たすとき,y=f(x) は区間 I で広義単調増加という。
-
任意の x1,x2∈I に対して,x1<x2 ならば f(x1)<f(x2) を満たすとき,y=f(x) は区間 I で狭義単調増加という。
→単調増加・単調減少の意味と覚えておくべき性質
三次関数の極値を計算する方法を2通り紹介します。
- 普通に代入する素直な方法
- 多項式の割り算を使う方法
→三次関数の極値を求める2通りの方法
基本方針
絶対値を含む不等式で表された領域は,絶対値の中身の正負で場合分けすることで,確実に図示できます。
→領域を図示するテクニック【絶対値つき不等式】
極大と極小の差
3次関数の極大値と極小値の差は 61 公式を使って高速に計算できる。
→3次関数の極大値と極小値の差をすばやく計算するテクニック

公式1:放物線
y=ax2+bx+c
上の二点
A,B
における接線の交点を
P
とおくとき,P
の
x
座標は
A,B
の
x
座標の平均となる
公式2:図において
S:T=2:1
である
→放物線の二接線の交点
シンプソンの公式
f(x)
が3次以下の関数のとき,
∫abf(x)dx=6(b−a){f(a)+4f(2a+b)+f(b)}
→シンプソンの公式の証明と例題
x32+y32=a32 で表される曲線をアステロイド曲線(星芒形)と呼ぶ。
→アステロイド曲線の重要な性質まとめ
シグモイド関数(Sigmoid Function)
シグモイド関数とは,
f(x)=1+e−ax1
という関数のこと。ただし,a>0 とする。
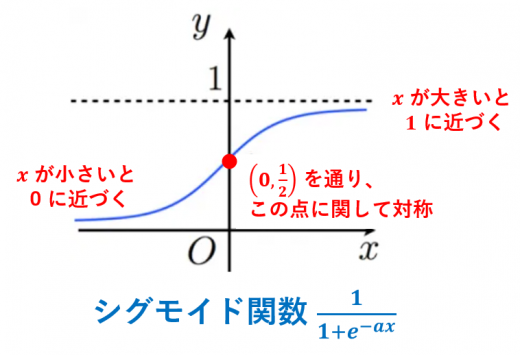
→シグモイド関数の意味と簡単な性質
中間値の定理
a≦x≦b
で連続な関数
f(x)
を考える。f(a)
と
f(b)
の間にある任意の実数
k
に対して,f(c)=k
となる
c(a≦c≦b)
が存在する。
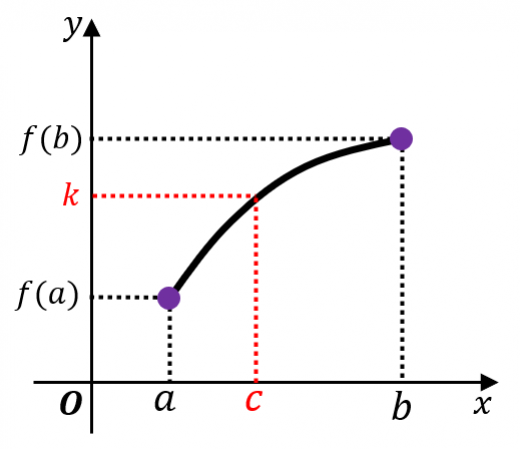
→中間値の定理の意味と多変数関数への応用
ラグランジュの未定乗数法
L(x,y,λ)=f(x,y)−λg(x,y)
とおくと,
(α,β) が極値を与えるならば,(α,β) は
- ∂x∂L=∂y∂L=∂λ∂L=0 の解。
または
- ∂x∂g=∂y∂g=0
の解。
→ラグランジュの未定乗数法と例題
定理
f(x)
が区間内で二階微分可能なとき,
- 下に凸
⟺
二階微分
f′′(x)≧0
- 上に凸
⟺
二階微分
f′′(x)≦0
→上に凸,下に凸な関数と二階微分
合成積(畳み込み)
合成積(畳み込み)は2つの関数から1つの関数を作る演算で,いろいろなところに登場する。

→合成積(畳み込み)の意味と応用3つ
テント写像
a
をパラメータとして,
f(x)=amin(x,1−x)
と表される関数(写像)をテント写像と言う。
→テント写像とその性質〜東大入試の背景〜
定点から三次関数のグラフに接線が何本引けるかを問う問題は頻出。図で覚えておくとよい。変曲点における接線が重要。
→三次関数の接線の本数についての美しい定理
多くの四次関数には二重接線が存在する。二重接線は平方完成を用いて簡単に求めることができる。
→四次関数の二重接線を素早く求める方法
カージオイド曲線の定義
極方程式 r=a(1+cosθ) で表される曲線をカージオイド曲線と言う。
→カージオイド曲線のグラフ,面積,長さ
包絡線の求め方
曲線群 f(x,y,t)=0 の包絡線の方程式は f(x,y,t)=0 と ∂t∂f(x,y,t)=0 から t を消去することで得られる。
→包絡線の求め方と例題
ファクシミリの原理
「x=k
と固定して
y
のとりうる値の範囲を求める」という操作を全ての
k
について行うことで,領域を求めることができる。
→ファクシミリの原理と通過領域の例題2問
逆双曲線関数
y=sinhx
の逆関数は,y=log(x+x2+1)
y=coshx(x≥0)
の逆関数は,y=log(x+x2−1)
(1≤x)
y=tanhx
の逆関数は,y=21log1−x1+x
(−1<x<1)
それぞれ arsinh,arcosh,artanh と表記することもあります。
→双曲線関数(sinhx, coshx, tanhx)の逆関数
二次元極座標平面上で
r=aebθ
と表される曲線を対数螺旋(または等角螺旋,ベルヌーイの螺旋)と言う。
→対数螺旋(等角螺旋)の長さと面積
1−x1=1+x+x2+⋯
(−1<x<1)
→1/(1-x) のテイラー展開と近似式
ハイポサイクロイドの媒介変数表示
x=(R−r)cosθ+rcos(θ−rRθ)
y=(R−r)sinθ+rsin(θ−rRθ)
→ハイポサイクロイド(特にデルトイド)の式と面積
ベジェ曲線
平面上における (N+1) 個の点 P0,P1,…,PN から以下の式で定まる曲線をベジェ曲線と呼ぶ。
p(t)=k=0∑NNCktk(1−t)N−kpk
ただし,t は実数で 0≦t≦1 の範囲を動く。
→ベジェ曲線の定義と4つの性質
定理
-
順像法(順手流・順手法・自然流)
変数を1つ固定し,他の変数に応じて図形がどのように動くか調べる。
-
逆像法(逆手流・逆手法)
各点 (x,y) に対して図形が通過するかどうか調べる。(存在条件を調べる)
→順像法と逆像法(自然法と逆手法)
アルキメデスの螺旋(らせん)
極方程式 r=aθ で表される曲線をアルキメデスの螺旋と呼ぶ。
→アルキメデスの螺旋
コーシー(cauchy)の関数方程式
f(x+y)=f(x)+f(y)
→コーシーの関数方程式の解法と応用
アッカーマン関数
A(m,n)
とは,非負整数
m,n
を入力とする二変数関数であり,m≥4
のときに猛烈に大きい値を取る。
→巨大数:アッカーマン関数とは
関数 f(x) に対して g(p)=xmax{px−f(x)} で定義される関数 g(p) を f(x) のルジャンドル変換と言う。
→ルジャンドル変換の意味と具体例
双曲線関数の加法定理
-
sinh(x+y)=sinhxcoshy+coshxsinhy
-
sinh(x−y)=sinhxcoshy−coshxsinhy
-
cosh(x+y)=coshxcoshy+sinhxsinhy
-
cosh(x−y)=coshxcoshy−sinhxsinhy
-
tanh(x+y)=1+tanhxtanhytanhx+tanhy
-
tanh(x−y)=1−tanhxtanhytanhx−tanhy
→双曲線関数の加法定理とその証明
練習問題
{x(θ)=3sinθy(θ)=2sin(2θ+6π)
と表されるリサージュ曲線で囲まれた領域の面積を求めよ。
→リサージュ曲線の定義とそれに関連する話
クロソイド曲線
媒介変数 t を用いて x(t)=∫0tcosθ2dθ,y(t)=∫0tsinθ2dθ と表される曲線はクロソイド曲線と呼ばれる。
→クロソイド曲線の性質とその証明
ニコメデスのコンコイド
ニコメデスのコンコイドとは
(x−b)2(x2+y2)=a2x2
で表される曲線である。
→ニコメデスのコンコイド
定理
パスカルの蝸牛形(蝸牛線・リマソン・limaçon of Pascal)とは
(x2+y2−ax)2−b2(x2+y2)=0
と表される曲線である。
→パスカルの蝸牛形(リマソン)
定理
シッソイド(疾走線)とは
x3+(x−a)y2=0
で表される曲線である。
→シッソイド(疾走線)
定理1(ミニマックス原理)
最高次の係数が 1 である n 次関数
P(x)=xn+an−1xn−1+⋯+a1x+a0
の中で,x 軸に [−1,1] で最も「近い」もの。つまり
−1≦x≦1max∣P(x)∣
を最小にするものはただ一つ存在し,それはチェビシェフ多項式 Tn(x) の定数倍 2n−11Tn(x) である。
→最良近似多項式に関するおもしろい定理
ここまでのまとめ
- max は最大値,arg max は最大値を与える値の集合
- max は値,arg max は集合
→argmax,argminの意味と例
ソフトマックス関数
ソフトマックス関数とは
yi=ex1+ex2+⋯+exnexi(i=1,…,n)
という関数のこと。
 各成分が正で,合計が 1 になるように調整するという役割を持つ。
各成分が正で,合計が 1 になるように調整するという役割を持つ。
→ソフトマックス関数
ランプ関数
f(x)={x0x≥0x<0
で表される関数をランプ関数と言う。

→ランプ関数(ReLU,正規化線形関数)









 各成分が正で,合計が になるように調整するという役割を持つ。
各成分が正で,合計が になるように調整するという役割を持つ。





