アルキメデスの螺旋
極方程式 で表される曲線をアルキメデスの螺旋と呼ぶ。
螺旋は「らせん」と読みます。
アルキメデスの螺旋(アルキメデスの渦巻線)についての知識を整理しました。
グラフ
グラフ
以下, の範囲で考えます。
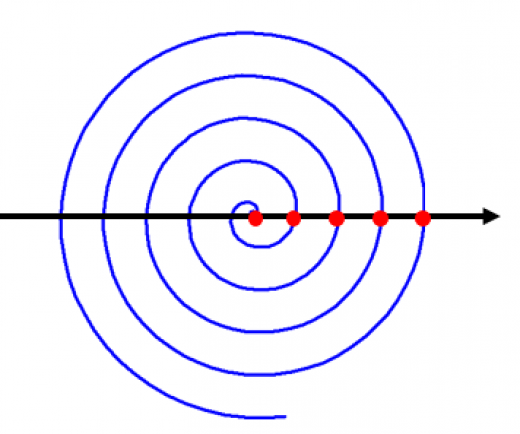 アルキメデスの螺旋のグラフは図のようになります。一回転するごとに が 増えます。つまり「赤い点の間隔が一定の螺旋」になります。
アルキメデスの螺旋のグラフは図のようになります。一回転するごとに が 増えます。つまり「赤い点の間隔が一定の螺旋」になります。
関連する螺旋
「赤い点の間隔の比率が一定の螺旋」 は対数螺旋と呼ばれます。→対数螺旋(等角螺旋)の長さと面積
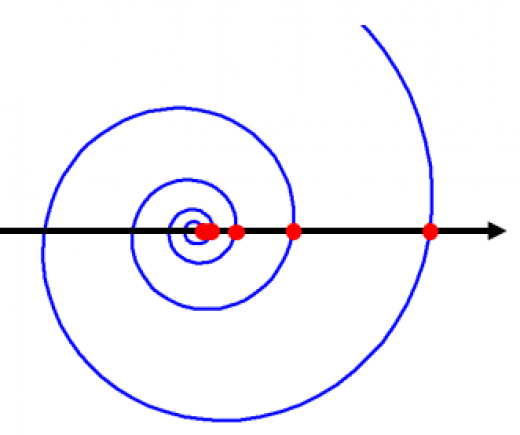
代表的な螺旋として2つセットで覚えておくとよいです。
長さ
長さ
アルキメデスの螺旋 において から までの長さは
ただし
なお,2002年度の京大で の場合が出題されています。ただし積分計算がしんどいので少し誘導がついていました。
面積
面積
アルキメデスの螺旋 において から まで動径が掃く面積は
媒介変数表示
媒介変数表示
は,アルキメデスの螺旋の媒介変数表示である。
極座標表示と 座標表示の間の関係式: より, という媒介変数表示が得られる。
直交座標表示
直交座標表示
は,アルキメデスの螺旋の 直交座標表示である。
より,
また
以上を に代入すると
対数螺旋をフリーハンドで描くのは難しいですがアルキメデスの螺旋なら描きやすいです。











