シグモイド関数の意味と簡単な性質
シグモイド関数とは,
という関数のこと。ただし, とする。
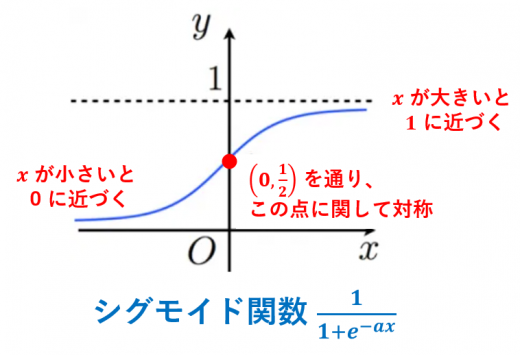
シグモイド関数のグラフ・性質・重要性(工学的な応用)について解説します。
シグモイド関数のグラフ
シグモイド関数のグラフ
シグモイド関数 のグラフは,以下のようになります。
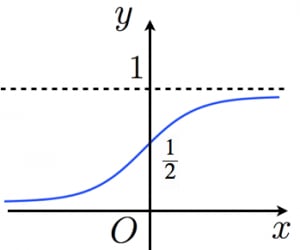
が大きいほどカーブが急激になり, が に近いほどなだらかな曲線になります。
シグモイド関数の性質
シグモイド関数の性質
シグモイド関数には以下の性質があります。
-
-
,
-
は単調増加
-
。つまり は に関して点対称。
それぞれ簡単な計算で確認できます。実際,グラフを見てみると1~4が成り立っていますね。

微分
微分
シグモイド関数 に対して となる。
つまり,シグモイド関数の微分は,シグモイド関数そのもの を使って簡単に表せます。
商の微分公式を使って計算すると,
シグモイド関数とtanh
シグモイド関数とtanh
-
シグモイド関数は を用いて表すこともできます:
-
ただし, はハイパボリックタンジェントと読み,定義は です。→双曲線関数(sinh,cosh,tanh)の意味・性質・楽しい話題まとめ
ステップ関数,符号関数
ステップ関数,符号関数
ここからはシグモイド関数の応用の話です。
シグモイド関数には不連続だがよく使う関数をなめらかな関数で近似するという役割があります。
例えば,工学的に重要な関数としてステップ関数,符号関数があります:
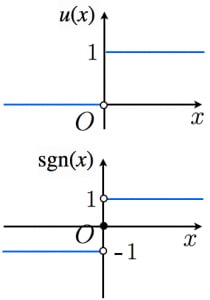
-
(単位)ステップ関数
-
符号関数
スイッチの切り替えを表現したり,いかにも使いそうな関数です。
連続近似
連続近似
ステップ関数や符号関数のように不連続な関数は扱いにくいことがあるので連続関数で近似したくなります。場合によっては微分可能であって欲しいこともあります。

- そこで,折れ線でつなぐことで「ステップ関数っぽい連続関数」(赤)を作ることができます。
- さらに,シグモイド関数を使うことで「ステップ関数っぽいなめらかな関数」(緑)を作ることができます。
符号関数も同様にシグモイド関数を2倍して1を引いたもの()を使うことで「符号関数っぽいなめらかな関数」が作れます。
また,シグモイド関数の が大きいほどよい近似になります。そして,なめらかな関数で近似する方法はたくさんありますが,シグモイド関数は数式も扱いやすい(例えば導関数をもとの関数で表せる)のでよく使われています。
シグモイド関数は,深層学習モデルにおける活性化関数としても使われる重要な関数です。
Tag:大学入試で頻出の有名な関数まとめ











