領域における最大・最小問題(線形計画法)
一次不等式で表される領域内で一次関数の値を最大化(または最小化)する問題を線形計画法(Linear Programming, LP)と言う。
領域内で関数の最大値,最小値を求める問題は入試でも頻出ですが,工学的な応用上も重要な問題です。
領域内で関数を最大化する例題
領域内で関数を最大化する例題
二変数の場合の線形計画法は入試で頻出です。まずは具体例。
,,, で表される領域内で関数 を最大にする点とその最大値を求めよ。
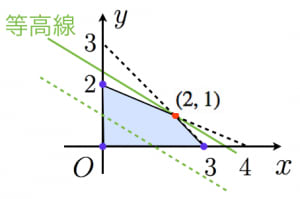
1:まずは不等式で表される領域を図示する。三つ目の不等式は の下側,四つ目の不等式は の下側の領域を表す。二つの直線の交点は である。以上から が動ける領域は図の青色の部分(境界含む)。
2:等高線 を書いてみる。
。よって,傾き で切片が であるような直線上の点は の値が となる。
よって領域内の点を通り傾きが の直線を引く。そのとき 切片が最大となるように頑張る(緑色の線)。そのときの直線と領域の交点が関数の最大値を与える点である。
3:きちんと議論する。
領域と交わる傾き の直線で一番切片が大きくなる(上側にある)のは図より を通るときである(三本の直線の傾きについて であることに注意する※)。
よって, で最大値を取り,その値は である。
領域の端点で最大値を取る
領域の端点で最大値を取る
- ベクトルの内積を使えば「 を最大化したい の方向に進みたい」とみなせます。例えば上記の例題では「領域内でベクトル の方向に進みたい」という問題になります。このように考えても答えが であることが分かります。→正射影ベクトルの公式の証明と使い方
- 当然ですが,目的関数の係数によっては関数の最大値を達成する点が変わってきます。そのため上記の例題では傾きの議論(※の部分)が必要になります。
- 例えば今回は赤い点が答えでしたが,関数が異なる場合,他の点(紫の点)で最大となることもあります。しかし「領域の端っこ(頂点)」で最大値,最小値を取るというのは(最適値が有界でないなどの例外を除いて)成り立ちます。
領域における最大・最小問題
領域における最大・最小問題
-
領域を表す不等式が一次式であり,最大化(最小化)したい関数も一次関数なので最も扱いやすい問題です。このように不等式も目的関数も一次式であるような問題を線形計画法と呼びます。
-
関数 を最大化するのと を最小化するのは同じなので最大化問題と最小化問題は本質的に同じです。
-
上記の例題の考え方(直線を動かして切片を最大化する)は最大化したい関数 が一次関数であれば,領域が曲がっていても使えます。例えば領域が「円の内部」とか「楕円の内部」などの問題も出題されます。
n変数の線形計画法
n変数の線形計画法
ここからは完全に余談です。
入試で出題されるのは二変数の線形計画法ですが, 一般に 変数の線形計画問題も考えられます。これは工学的にも非常に重要な問題です。工学的に重要だからこそ大学入試で出題されやすいのかもしれません。
二変数の線形計画法の場合 平面でものごとを考えることができましたが, 変数の場合 次元空間で考える必要があります。 の場合はもはや不等式で表される領域を図示することができません。そもそも4次元空間ってなんだよって話ですよね。
しかし,現代のテクノロジーを使えば 変数の線形計画法も高速に解くことができます。例えば,二変数の場合と同様「最大値(最小値)を取るのは領域の端っこ」であることを利用した単体法という解法があります。他にも内点法や楕円体法などの解法もあり,世の中の多くの問題が線形計画法の形で定式化され,実際に解かれています。
様々な制約のもとで関数を最大化,最小化する数学の一分野を「最適化」と言います。
Tag:数学的モデリングまとめ(線形計画法)











