順像法と逆像法（自然法と逆手法）

イメージ

通過領域を求める問題では，変数（例えば ttt）を代入すると，それに応じた図形 CtC_tCt​ が得られます。
この対応を「関数」だと思いましょう。
順像法は，ttt を入れて出てきたものを観察する方法です。
逆像法は，この (x,y)(x,y)(x,y) が出力される ttt は存在するだろうかと考察する方法です。
さて，実際に具体的な計算例を見ていきましょう。

例題

次の例題を用いて解説します。

例題

$t$ が実数全体を動くとき，直線 $y = 2tx - t^2$ の通過領域を求めよ。
$t$ が $0 \leqq t \leqq 2$ の範囲を動くとき，直線 $y = 2tx - t^2$ の通過領域を求めよ。

イメージ図

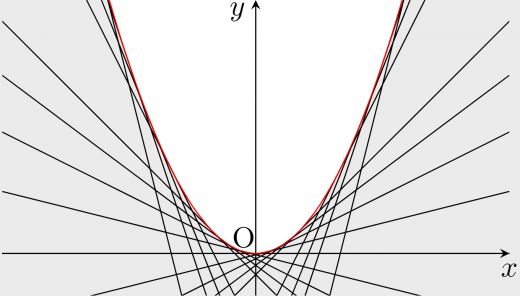
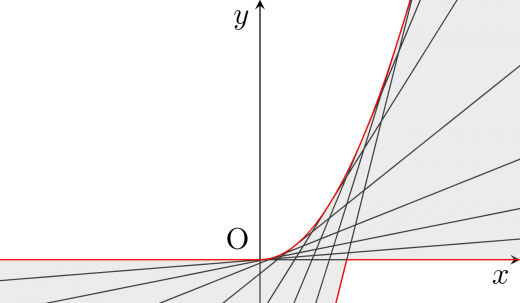
順手法

まずは順手法で解いてみます。

1の解

求める通過領域を $C$ とする。

$C$ を直線 $x=k$ での切り口の $y$ 座標の範囲を求める。

直線の式に $x=k$ を代入すると $\begin{aligned} y &= 2tk - t^2\\ &= -(t-k)^2 + k^2 \end{aligned}$ である。

$t$ は任意の実数値を取るので $y \leqq k^2$ である。

よって $C$ は $y \leqq x^2$ となる。

2の解

1の計算同様にすると $x = k$ において $y = -(t-k)^2 + k^2$ となる。

$f(t) = -(t-k)^2 - k^2$ とおく。二次関数の軸は $t = k$ となる。

$k < 0$ のとき
$t = 2$ のとき最小値 $4k-4$ ， $t = 0$ のとき最大値 $0$ を取る。
$0 \leqq k \leqq 1$ のとき
$t = 2$ のとき最小値 $4k-4$ ， $t = k$ のとき最大値 $k^2$ を取る。
$1 < k \leqq 2$ のとき
$t = 0$ のとき最小値 $0$ ， $t = k$ のとき最大値 $k^2$ を取る。
$2 < k$ のとき
$t = 0$ のとき最小値 $0$ ， $t = 2$ のとき最大値 $4k-4$ を取る。

以上をまとめると $\begin{cases} 4x-4 \leqq y \leqq 0 &(x < 0)\\ 4x-4 \leqq y \leqq x^2 &(0 \leqq x \leqq 1)\\ 0 \leqq y \leqq x^2 &(1 < x \leqq 2)\\ 0 \leqq y \leqq 4x-4 &(2 < x) \end{cases}$ となる。

$x=k$ での切り口を考えて解きました。このような手法は順手法の中でもファクシミリの原理と呼ばれます。
→ファクシミリの原理と通過領域の例題２問

逆手法

1の解

通過領域を $C$ とする。

$(X,Y) \in C$ とする。このとき，ある $t$ があって，直線 $y = 2tx - t^2$ 上に $(X,Y)$ がある。

ゆえに

$(X,Y) \in C$ $\iff$ $Y = 2tX - t^2$ を満たす実数 $t$ が存在

となる。式を変形することで

$(X,Y) \in C$ $\iff$ $t^2 - 2tX + Y = 0$ を満たす実数 $t$ が存在

となる。 $t^2 - 2tX + Y = 0$ の判別式を $D$ とすると $D = X^2 - Y$ となる。

以上をまとめると

$(X,Y) \in C \iff D \geqq 0$ すなわち $Y \leqq X^2$

である。

よって $C$ は $y \leqq x^2$ となる。

2の解

1と同様に考えると， $t^2 - 2tX + Y = 0$ が $0 \leqq t \leqq 2$ の範囲に解を持つ条件を求めればよい。

$f(t) = t^2 - 2tX + Y$ とおく。

$f(t) = (t-X)^2 - X^2 + Y$

$X,Y$ を自由に動かしたときの $f(t)$ の $0\leqq t\leqq 2$ での最小値が $0$ より以下で，最大値が $0$ 以上である条件を求めるとよい。

$X < 0$ のとき
$f$ は $t=2$ のとき最大値 $4-4X+Y$ ， $t=0$ のとき最小値 $Y$ を取る。
よって，求めるべき条件は $4-4X+Y \geqq 0$ ， $Y \leqq 0$ である。
$0 \leqq X \leqq 1$ のとき
$f$ は $t=2$ のとき最大値 $4-4X+Y$ ， $t=X$ のとき最小値 $Y-X^2$ を取る。
よって，求めるべき条件は $4-4X+Y \geqq 0$ ， $Y-X^2 \leqq 0$ である。
$1 < X \leqq 2$ のとき
$f$ は $t=0$ のとき最大値 $Y$ ， $t=X$ のとき最小値 $Y-X^2$ を取る。
よって，求めるべき条件は $Y \geqq 0$ ， $Y-X^2 \leqq 0$ である。
$2 < X$ のとき
$f$ は $t=0$ のとき最大値 $Y$ ， $t=2$ のとき最小値 $4-4X+Y$ を取る。
よって，求めるべき条件は $Y \geqq 0$ ， $4-4X+Y \leqq 0$ である。

以上をまとめると $\begin{cases} 4x-4 \leqq y \leqq 0 &(x < 0)\\ 4x-4 \leqq y \leqq x^2 &(0 \leqq x \leqq 1)\\ 0 \leqq y \leqq x^2 &(1 < x \leqq 2)\\ 0 \leqq y \leqq 4x-4 &(2 < x) \end{cases}$ となる。

どっちでやるのが簡単？

順手法と逆手法のどちらで解くのが簡単か，それは問題によります。

例えば先ほどの例題はどちらで解いても難易度はそこまで変わりません。

それではここからの例題2問，それぞれどちらでやるのが簡単か，考えてみましょう。

例題2

$x,y$ がそれぞれ $x > 0, y < 1$ の範囲で動くとき，点 $(X,Y) = (x+y,xy)$ の動く範囲を求めよ。

これは逆手法で解きましょう。本問のように変数が複数ある場合は，順手法は難しいです。

解答

求める領域を $C$ とおく。

$t^2 - Xt + Y = 0$ は $x,y$ を解に持つ二次方程式である。

この方程式が $1$ より小さい解と $0$ より大きい解の2解を持つ条件を調べる。

特に，2解が共に $1$ 以上のときと，2解が共に $0$ 以下の場合を求めれば，その補集合が $C$ である。

方程式の判別式を $D$ とおくと， $D = X^2 - 4Y$ である。よって，実数解を持つためには $Y \leqq \dfrac{1}{4} X^2$ が必要となる。

以下， $f(t) = t^2 - Xt + Y$ とおく。

(i) 2解が $1$ 以上のとき

条件は

$f(1) \geqq 0$ ，対称軸について $\dfrac{X}{2} \geqq 1$

の2つである。それぞれ

$Y \geqq X-1$ ， $X \geqq 2$

と表される。

(ii) 2解が $0$ 以下のとき

条件は

$f(0) \geqq 0$ ，対称軸について $\dfrac{X}{2} \leqq 0$

の2つである。それぞれ

$Y \geqq 0$ ， $X \leqq 0$

と表される。

以上より求める範囲は $\begin{cases} Y < 0 &(X \leqq 0)\\ Y \leqq \dfrac{1}{4} X^2 &(0 < X < 2)\\ Y < X-1 &(2 \leqq X) \end{cases}$ となる。

図示すると下図のようになる。（点線は含まない）

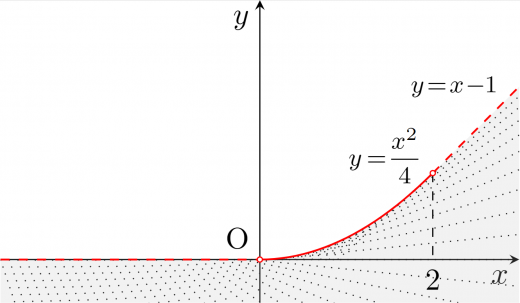
（なお，上図ではイメージしやすいように点を打ってあるが，実際に答案にする際に描く必要はない）

それでは次の問題です。

例題3

実数 $t$ は $0 \leqq t \leqq 1$ の範囲を動く。このとき，2点 $(t,t^2)$ ， $(t+1,0)$ を通る直線が通過する領域を求めよ。

一見逆手法のほうが簡単に見えます。

実際に直線の式を計算すると $\begin{aligned} y &= -t^2 (x-t) + t^2\\ &= -t^2 x + t^3 + t^2 \end{aligned}$ となり， $t$ の3次式について考察することになります。

2次なら判別式を考えて計算できますが，今回はやや大変そうです。というわけで順手法でいきましょう。

解

求める領域を $C$ とする。

直線の式は $y = -t^2 x + t^3 + t^2$ である。

$x = k$ で $C$ を切ったとき，その切り口の $y$ 座標は $y = t^3 - (k-1) t^2$ と表される。

$\begin{aligned} y' &= 3t^2 - 2(k-1) t\\ &= 3 t \left( t - \dfrac{2}{3} (k-1) \right) \end{aligned}$ であるため， $t = 0 , \dfrac{2}{3} (k-1)$ で極値をとる。

$\dfrac{2}{3} (k-1) \leqq 0$ すなわち $k \leqq 1$ のとき
増減表は $\begin{array}{c|ccc} t & 0 & \cdots & 1\\ \hline y' & 0 & + & +\\ \hline y & 0 & \nearrow & 2-k \end{array}$ である。
$0 \leqq \dfrac{2}{3} (k-1) \leqq 1$ すなわち $1 \leqq k \leqq \dfrac{5}{2}$ のとき
増減表は $\begin{array}{c|ccccc} t & 0 & \cdots & \dfrac{2}{3} (k-1) & \cdots & 1 \\ \hline y' & 0 & - & 0 & + & \\ \hline y & 0 & \searrow & -\dfrac{4}{27} (k-1)^3 & \nearrow & 2-k \end{array}$ である。
$\dfrac{2}{3} (k-1) \geqq 1$ すなわち $k \geqq \dfrac{5}{2}$ のとき
増減表は $\begin{array}{c|ccc} t & 0 & \cdots & 1\\ \hline y' & 0 & - & -\\ \hline y & 0 & \searrow & 2-k \end{array}$ である。

増減表を元に値域をまとめると次のようになる。 $\begin{cases} 0 \leqq y \leqq 2-x &(x \leqq 1)\\ -\dfrac{4}{27} (x-1)^3 \leqq y \leqq 2-x &(1 \leqq x \leqq 2)\\ -\dfrac{4}{27} (x-1)^3 \leqq y \leqq 0 &\left( 2 \leqq y \leqq \dfrac{5}{2} \right)\\ 2-x \leqq y \leqq 0 &\left( \dfrac{5}{2} \leqq x \right) \end{cases}$

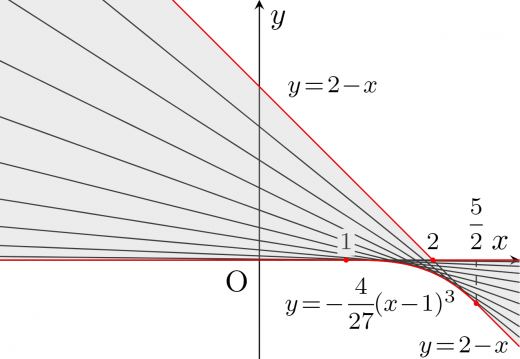
（なお，上図ではイメージしやすいように線を引いてあるが，実際に答案にする際に描く必要はない）

$+\alpha$ の話～包絡線について

$t$ などのパラメタに応じて動く曲線群に対して，全ての曲線と接する曲線のことを包絡線と言います。

詳しくは包絡線の求め方と例題をご覧ください。

その他例題

東京大学理科2021年大問1は軌跡の問題で，順手法・逆手法で解くことができます。是非トライしてみてください。 → 【解答・解説】東大理系数学2021

今回紹介した例題のように，二次関数や三次関数の解の問題に帰着されることが多いです。三角関数や対数関数に帰着される場合もあります。

イメージ

例題

イメージ図

順手法

逆手法

どっちでやるのが簡単？

+α+\alpha+α の話～包絡線について

その他例題

$+\alpha$ の話～包絡線について