ランプ関数（ReLU，正規化線形関数）

更新 2022/06/27

ランプ関数

$f(x)=\begin{cases}x&x\geq 0\\0&x< 0\end{cases}$

で表される関数をランプ関数と言う。

ランプ関数のグラフ

ランプ関数は，正規化線形関数，Rectified Linear Function，ReLU（レル）などとも呼ばれます。ニューラルネットワークの活性化関数として使われる場合はReLUと呼ばれることが多いです。

他の表現

ランプ関数は， $f(x)=\max (0,x)$ と表現することもできます。ただし， $\max (a,b)$ は $a$ と $b$ のうち大きい方（厳密には小さくない方）を返す関数です。
絶対値を使えば， $f(x)=\dfrac{x+|x|}{2}$ と表現することもできます。

ランプ関数の微分

x>0x>0x>0
 では
f′(x)=1f'(x)=1f′(x)=1
x=0x=0x=0
 で微分不可能
x<0x<0x<0
 では
f′(x)=0f'(x)=0f′(x)=0
となります。
y=f′(x)y=f'(x)y=f′(x)
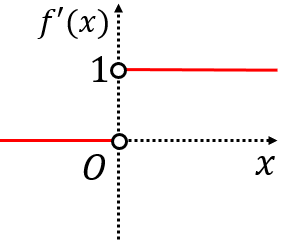
 のグラフは図のようになります。
シグモイド関数の意味と簡単な性質でも登場した単位ステップ関数とほとんど同じです。ただし，x=0x=0x=0
 では
f′(x)f'(x)f′(x) は定義されません。正確にはヘビサイドの階段関数と言います。

ラプラス変換

ここからは高校数学範囲外です。

ランプ関数をラプラス変換すると， $F(s)=\dfrac{1}{s^2}$ となる。

導出

ラプラス変換の定義に従って計算するのみ：

$F(s)=\displaystyle\int_{0}^{\infty}f(t)e^{-st}dt\\ =\displaystyle\int_0^{\infty}te^{-st}dt\\ =\left[t\dfrac{e^{-st}}{(-s)}\right]_0^{\infty}+\displaystyle\int_0^{\infty}\dfrac{e^{-st}}{s}dt\\ =\left[\dfrac{e^{-st}}{-s^2}\right]_0^{\infty}\\ =\dfrac{1}{s^2}$