最良近似多項式に関するおもしろい定理
最良近似多項式の意味と,関連するおもしろい定理を2つ紹介します。
最良近似多項式の例題
最良近似多項式の例題
まずは比較的易しい大学入試レベルの例題です。
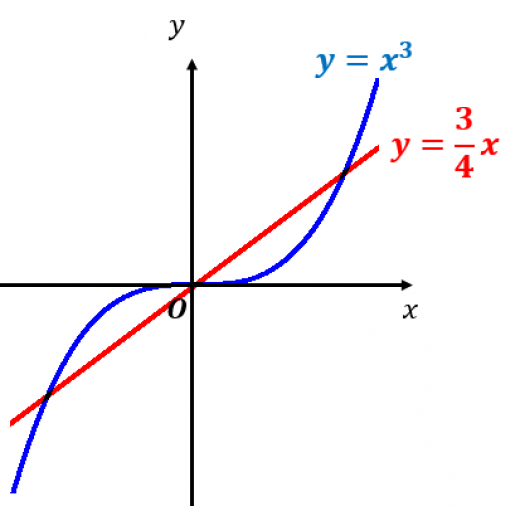
において に最も「近い」1次以下の関数 を求めよ。
ただし,「近さ」は差の最大値 で測るものとする。
まず, とすれば,差の最大値は になる。

これが唯一の最適解であることを示す。
もし,差の最大値が 以下なら
より
より
より
1つめと3つめの式より ,つまり
これと2つめの式より さらに1つめと2つめの式より がわかる。
この問題にあるように,考えている区間内で「最も遠いところを近くする」多項式を最良近似多項式と呼ぶことにします。
チェビシェフ多項式とミニマックス原理
チェビシェフ多項式とミニマックス原理
最良近似多項式に関連する定理です。定理1を使えば問題1が一瞬で解けます。
最高次の係数が である 次関数
の中で, 軸に で最も「近い」もの。つまり を最小にするものはただ一つ存在し,それはチェビシェフ多項式 の定数倍 である。
チェビシェフ多項式とは, となる多項式 です。コサインの 倍角の公式から定まります。例えば,
- より
- より
です。 は最高次の係数が である 次多項式です。つまり, は最高次の係数が になるように定数倍したチェビシェフ多項式です。
では定理1を使ってみましょう。
のときの定理1から分かる。つまり,
を最小にするのは であるので, に最も「近い」1次以下の関数は
のときもやってみる。
を最小にするのは であるので, に最も「近い」2次以下の関数は
同様に, に最も「近い」 次以下の関数も計算できます。
定理1の補足
- 定理1はマックスを最小(ミニマム)にする問題に関するのでミニマックス原理と呼ばれることがあります。
- 定理1の証明については後述します。
交代定理
交代定理
ここからさらに一般論です。
交代定理,あるいは等振動定理(Equioscillation theorem)と呼ばれるおもしろい定理です。
区間 上で定義された( 次以下の多項式ではない)連続関数 を考える。このとき, に最も「近い」 次以下の多項式がただ1つ存在し,それは以下の条件を満たす。
条件: に最も「遠い」 点からなる交代点列が存在する。つまり, 相異なる 点 が存在して,
- に対して を満たす,かつ
- の符号が交代的( から までプラスとマイナスが交互)
さらに,上記の条件を満たす 次以下の多項式 はただ1つである。
最も「遠い」点がたくさん( 次多項式なのに 個)あり,それが上下交互になるようにいろいろな場所のバランスを調整するイメージです。
定理2を認めれば定理1を導出できます。
,, として定理2を使う。
に で最も「近い」 次以下の多項式がただ1つ存在し,以下の条件を満たす。
条件:相異なる 点 が存在して, に対して かつ符号が交代的。
あとは, のときにこの条件を満たすことを示せばよい。
であり,これが最大になるのは のときで 点あり符号も交代的なのでOK。
( を から まで動かすと, は から まで動く。 は振動しながら, で絶対値最大の を交互に取る)
参考文献として紹介したPDFは少し難しいですが最高なのでぜひ読んでみてください。











