ハイポサイクロイド（特にデルトイド）の式と面積

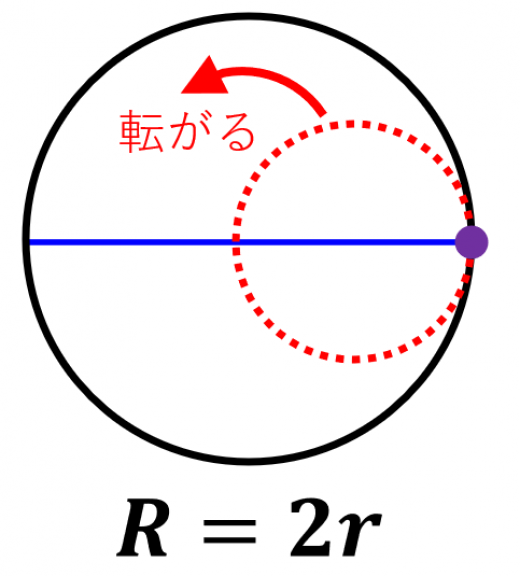
半径 $R$ の定円の内側を半径 $r\:(<R)$ の円が転がる状況を考えます。 図のように，赤い円が反時計回りに公転（時計回りに自転）します。

このとき，転がる円周上の1点 $P$ が描く軌跡（青い曲線）は以下の式で表せます。

• ただし，半径 $R$ の円の中心を原点とし，$P$ は転がる前の2つの円の接点 $(R,0)$ とします。
• この曲線をハイポサイクロイドまたは内サイクロイドと言います。

なお，第二項の位相をプラスにするために $$x=(R-r)\cos\theta+r\cos(\frac{R}{r}\theta-\theta)$$ $$y=(R-r)\sin\theta-r\sin(\frac{R}{r}\theta-\theta)$$ と書くこともできますが，位相をプラスにしない方が式がきれい かつ 意味がわかりやすいと思います。

• $R=2r$ の場合 $$x=r\cos\theta+r\cos(-\theta)=2r\cos\theta$$ $$y=r\sin\theta+r\sin(-\theta)=0$$ となり，$x$ 軸の一部（線分）を表します。

• $R=3r$ の場合 $$x=2r\cos\theta+r\cos(2\theta)$$ $$y=2r\sin\theta-r\sin(2\theta)$$ となります。これはデルトイド(Deltoid)と呼ばれる曲線です。

• $R=4r$ の場合 $$x=3r\cos\theta+r\cos(3\theta)=4r\cos^3\theta$$ $$y=3r\sin\theta-r\sin(3\theta)=4r\sin^3\theta$$ となります。三倍角の公式を使ってきれいになるのが楽しいです。これはアステロイド(Asteroid)と呼ばれる曲線です。

ただし，$n$ は $2$ 以上の整数とします。

• $n=2$ の場合，曲線は線分であり確かに $S=0$ です。
• $n=4$ の場合，$S=6r^2=\dfrac{3}{8}R^2$ です。これはアステロイド曲線の重要な性質まとめ で計算した結果 と一致しています。
• $n$ が十分大きいとき，つまり転がる円が小さいとき，$$S=\dfrac{(n-1)(n-2)}{n^2}\pi R^2\fallingdotseq \pi R^2$$ となり，ほぼ定円の面積と同じです。
• $n=3$（デルトイド）の場合で確認してみます。

ガウスグリーンの定理を使って計算することもできますが，計算は大変です。

一般の $n$ に対しても同様に計算できます。

• 定円の内側を円が転がるとき，円周上の1点が描く軌跡がハイポサイクロイド（内サイクロイド）でした。
• 定円の外側を円が転がるとき，円周上の1点が描く軌跡はエピサイクロイド（外サイクロイド）と言います。エピサイクロイドの例としては，カージオイドがあります。
• 直線を円が転がるとき，円周上の1点が描く軌跡はサイクロイドです。
• 定円の内側を円が転がるとき，転がる円の内部（または外部）の1点が描く軌跡を内トロコイドと言います。外トロコイドも同様です。