指数・対数関数 に関する26記事をまとめました。くわしくは各リンク先を見てください。
対数の基本公式
対数の定義:ab=c⟺logac=b
-
logaM+logaN=logaMN
-
logaMp=plogaM
-
logaM1=−logaM
-
logaM−logaN=logaNM
-
loga1=0
-
logab=logcalogcb(底の変換公式)
→覚えておきたい対数(log)の応用公式4点セット
覚えておくと便利な常用対数
- log102≒0.3010
- log103≒0.4771
- log107≒0.8451
- logex≒2.3log10x
→常用対数の覚え方と検算への応用
方針1
指数関数のグラフは,以下の三点を調べて,それをいい感じにつなげれば簡単に書ける
- x が十分小さいとき(x→−∞)
- x=0 のとき
- x が十分大きいとき(x→∞)
→指数関数のグラフの二通りの書き方
正の実数
a
と実数
x
に対して,ax
を以下のように定義する:
-
x
が正の整数のとき,ax=
(a
を
x
回かけたもの)
-
x
が
0
のとき,ax=1
-
x
が負の整数のとき,ax=a−x1
-
x
が有理数
pq
のとき,ax=(pa)q
-
x
が無理数のとき,f(x)=ax
が連続関数になるようにつなげる
→ゼロ乗(0乗),マイナス乗,分数乗,無理数乗
底の変換公式
a,b,c>0,a,c=1 のとき
logab=logcalogcb
が成り立つ。
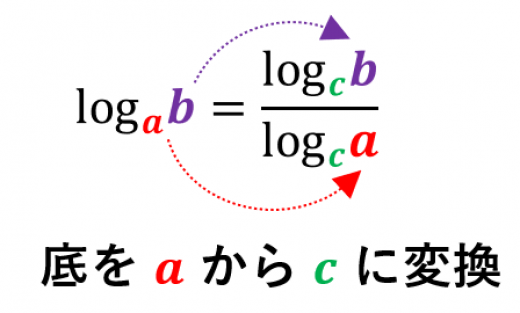
→底の変換公式の証明と例題
-
logaM+logaN=logaMN
-
logaMp=plogaM
-
logaM1=−logaM
-
logaM−logaN=logaNM
-
loga1=0
-
logab=logcalogcb
→対数の基本的な性質とその証明
次の関係式を指数法則という。
am×anam÷an(am)n(ab)n(ba)n=am+n=am−n=amn=anbn=bnan
→指数法則の直感的な意味と利用例
- 基本形
- 置換を利用して解く指数方程式
- 底が異なる指数方程式
- 指数方程式の連立方程式
→指数方程式の解き方
→指数不等式の解法
底と真数とは
対数 logab について,a のことを底,b のことを真数と言う。
→対数(log)の定義・計算方法・便利な公式まとめ
二乗・累乗・べき乗に関連した用語をわかりやすく解説します。
→二乗・累乗の特徴と対数との関係
例題
次の方程式を解け。
(1) log2(x+1)=2+log2x
(2) log9x=log3(x−2)
(3) (log2x)2=log2x2
(4) logx2=log2x2+1
→対数方程式の例題と解き方
例題
次の不等式を解け。
(1) log2(x+3)<2log2(x+1)
(2) log0.5x+1≧log2(x+1)
(3) (log2x)2≦log2x+2
→対数不等式の例題と解き方
1の三乗根
3乗して 1 になる複素数は3つある。具体的には,
1 と 2−1±3i
→三乗根(立方根)の意味と計算をわかりやすく
常用対数
常用対数とは,10 を底とする対数
log10N
のこと。
つまり,10x=N を満たす x のこと。
→常用対数の意味と計算(桁数・最高位の数)
数 a に対して,n 乗して a になるような数を a の n 乗根という。
→累乗根の定義と具体例
(i)
ex≧1
(ii) ex≧1+x
(iii)
ex≧1+x+2x2
(iv)
ex≧1+x+2x2+6x3
ただし,(i)と(iii)は,x≧0
の範囲で成立する不等式で,(ii)と(iv)はすべての実数
x
に対して成立します。
→マクローリン展開にまつわる指数関数の不等式
双曲線関数
双曲線関数と呼ばれる重要な関数 cosh,sinh,tanh が以下の式で定義される:
- coshx=2ex+e−x
- sinhx=2ex−e−x
- tanhx=coshxsinhx=ex+e−xex−e−x
→双曲線関数(sinh,cosh,tanh)の意味・性質・楽しい話題まとめ
y=e−axsinbx
およびy=e−axcosbx
は減衰曲線と呼ばれる重要な関数。
→減衰曲線の重要な性質まとめ
ネイピア数の定義
数列
an=(1+n1)n
の n→∞ での極限は存在する。その値を自然対数の底(ネイピア数)と呼び,e と書く。
→自然対数の底(ネイピア数)の定義:収束することの証明
性質1
n→∞limnn=1
→nのn乗根の最大項と極限
→ネイピア数eが無理数であることの証明
有名不等式
任意の正の実数 x に対して
logx≦x−1
→有名不等式logx≦x-1の証明と入試問題
懸垂線(カテナリー)
ひもの両端を手で持ってたらした曲線の式は
y=2a(eax+e−ax)
この曲線を懸垂線またはカテナリーと呼ぶ。
→懸垂線の2通りの導出
双曲線関数のマクローリン展開
sinhxcoshxtanhx=x+3!x3+5!x5+⋯=1+2!x2+4!x4+⋯=x−31x3+152x5−⋯
→双曲線関数(sinh,cosh,tanh)のマクローリン展開を3通りの方法で計算
指数関数のマクローリン展開
ex=1+x+2!x2+3!x3+4!x4+⋯
→e^xのマクローリン展開,三角関数との関係