常用対数の意味と計算（桁数・最高位の数）

更新 2024/08/01

常用対数の意味と応用例を紹介します。常用対数を使えば「 $2^{30}$ の桁数を計算せよ」のような問題も解けます。

常用対数とは

常用対数

常用対数とは， $10$ を底とする対数 $\log_{10}N$ のこと。

つまり， $10^x=N$ を満たす $x$ のこと。

例

$10^2=100$ であるので $\log_{10}100=2$

$10^3=1000$ であるので $\log_{10}1000=3$

このように，常用対数 $\log_{10}N$ は $10$ を何乗したら $N$ になるか？を表す数とも言えます。

常用対数の計算

$\log_{10}2\fallingdotseq 0.3010$ ， $\log_{10}3\fallingdotseq 0.4771$ など計算に必要な値は問題文で与えられます。覚えておいても良いです。→常用対数の覚え方と検算への応用
→高校数学の問題集　～最短で得点力を上げるために～のT70は，常用対数の近似値を覚えておけば検算できます。
また，以下の対数の公式を使うことも多いです。

対数の性質

$\log_aMN=\log_aM+\log_aN$

$\log_a\dfrac{M}{N}=\log_aM-\log_aN$

$\log_a M^r = r \log_a M$ 　( $r$ は実数)

詳細は→対数(log)の定義・計算方法・便利な公式まとめ

例

$\log_{10}12$ を計算してみよう。

まず対数の公式を使うと

$\begin{aligned} \log_{10}12 &= \log_{10} (2^2\times 3)\\ &=\log_{10}2^2+\log_{10}3\\ &=2\log_{10}2+\log_{10}3 \end{aligned}$

ここで $\log_{10}2\fallingdotseq 0.3010$ ， $\log_{10}3\fallingdotseq 0.4771$ を使うと，

$2\times 0.3010+0.4771=1.0791$ となる。

常用対数表

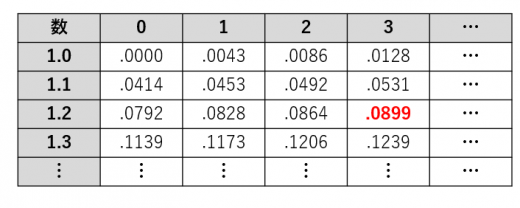
常用対数表を使うこともあります。例えば $\log_{10}1.23$ を求めたいときは，

小数第一位までの値 $1.2$ の行を探し
小数第二位の値 $3$ の列を探し
その行と列に対応する値 $0.0899$ を読み取る

という手順で $\log_{10}1.23\fallingdotseq 0.0899$ がわかります。常用対数表

常用対数を使って桁数を求める

常用対数を用いることで，大きな数の桁数を計算できます。

例えば，

$N$ が $3$ 桁の数
$\iff 100\leqq N< 1000$
$\iff 2\leqq\log_{10} N < 3$

となります。より一般に，以下の公式が成立します。

桁数を求めるための公式

正の整数 $N$ が $n$ 桁の数
$\iff 10^{n-1} \leqq N < 10^n$
$\iff n-1\leqq \log_{10}N < n$

2行目では，左側は等号つき不等号，右側は等号なし不等号です。2行目の各辺の常用対数を取ると3行目になります。

例題

$N=2^{30}$ の桁数を求めよ。ただし， $\log_{10}2=0.3010$ として計算せよ。

解答

$N$ の常用対数を取ると，

$\log_{10}2^{30}=30\log_{10}2=9.030$

よって， $9\leqq \log_{10} 2^{30}< 10$ なので桁数を求めるための公式より $2^{30}$ は $10$ 桁の数である。

別解（余談）

本筋からそれるが， $2^{30}$ くらいなら自力で計算できる。 $2^{10}=1024$ は多くの人が覚えているだろう。よって $1000^{3} < 2^{30} < 2000^{3}$ となる。 $1000^3$ と $2000^3$ は $10$ 桁の数なので $2^{30}$ も $10$ 桁の数。

注： $2^{10}=1024$ はぜひ覚えておきましょう。特に情報系の人が喜ぶキリのいい数です。

常用対数を使って最高位の数を求める

次はもう少し難しい常用対数の応用方法です。常用対数を使って最高位の数を計算できます。最高位の数とは，一番左側の数字です。例えば， $3456$ の最高位の数は $3$ です。

例えば，

$N$ が $4$ 桁の数で最高位の数が $6$
$\iff 6000 \leqq N < 7000$
$\iff 3+\log_{10} 6\leqq \log_{10}N < 3+\log_{10}7$

となります。より一般に以下の公式が成立します。

最高位の数を求めるための公式

$N$ が $n$ 桁の数で最高位の数が $a$
$\iff a\cdot 10^{n-1} \leqq N < (a+1)\cdot 10^{n-1}$
$\iff n-1+\log_{10}a\leqq \log_{10}N < n-1+\log_{10}(a+1)$

$n=4,\:a=6$ とするとさきほどの例になります。

$\log_{10}N$ の整数部分が $n-1$ になります。つまり，小数部分を見れば最高位の数が分かるというわけです。

例題

$N=2^{30}$ の最高位の数を求めよ。ただし， $\log_{10}2=0.3010$ として計算せよ。

解答1

さきほど計算したように， $\log_{10}2^{30}=9.030$

小数部分 $0.03$ は $\log_{10}1=0$ より大きく $\log_{10}2=0.3010$ より小さい。

つまり， $9+\log_{10}1\leqq \log_{10}2^{30} < 9+\log_{10}2$

よって $10^{9}\leqq 2^{30} < 2\cdot 10^9$

つまり最高位の数は $1$ である。

解答2

これくらいの計算は突破できる気合いが欲しい。

$2^{30}=1024^3=1073741824$ なので最高位の数は $1$

気合いで計算するのが難しい例題

例題2

$6^{200}$ の桁数と最高位の数を求めよ。ただし， $\log_{10}2=0.3010$ ， $\log_{10}3=0.4771$ として計算せよ。

さすがに $200$ 乗ともなると気合いで計算するのは厳しいですね。

解答（桁数）

$\begin{aligned} &\log_{10}6^{200}\\ &=200(\log_{10}2+\log_{10}3)\\ &=155.62 \end{aligned}$

よって， $155\leqq \log_{10}6^{200}< 156$ より $10^{155}\leqq 6^{200} < 10^{156}$

よって $6^{200}$ は $156$ 桁である。

解答（最高位の数）

$\log_{10}6^{200}$ の小数部分は $0.62$ である。

$\log_{10}4=2\log_{10}2=0.6020$

$\log_{10}5=1-\log_{10}2=0.6990$

より， $155+\log_{10}4\leqq \log_{10}6^{200}< 155+\log_{10}5$

よって， $4\cdot 10^{155}\leqq 6^{200} < 5 \cdot 10^{155}$

つまり最高位の数は $4$ である。

注：ちなみに $6^{200}$ を実際に計算してみると，有効数字 $4$ 桁で $4.268\times 10^{155}$ となります。

小学生の頃，2のべき乗を休み時間の間ずっと計算して遊んだのを思い出します。

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！