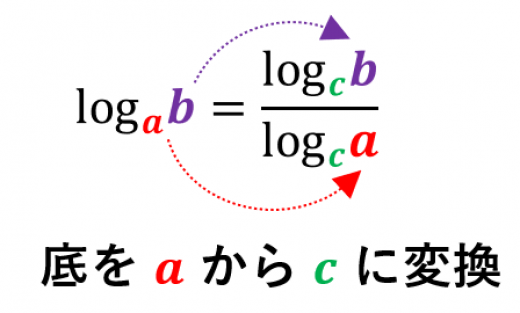例題
log48
を計算せよ。
解答
底の変換公式を使って底を
2
にするのがスタンダードな考え方。
log48=log24log28=log222log223=23
別解
スタンダードであるだけで,底は
2 である必要はない。なんでもよい。
log48=logc4logc8=logc22logc23=2logc23logc2=23
注:慣れていれば普通に
423=8
より
log48=23,と一瞬で計算できます。
例題2
log35log57log79
を計算せよ。
解答
底は何でもいいが,9=32 で 5,7 は素数であることから
3
にそろえるのがオススメ。
log35log57log79=log33log35log35log37log37log39=log33log39=2
別解
もちろん底は
3
である必要はない。なんでもよい。
log35log57log79=logc3logc5logc5logc7logc7logc9=logc3logc9=logc3logc32=logc32logc3=2
なお,覚えておきたい対数(log)の応用公式4点セットの公式(ii)を使えば一発で
log35log57log79=log39=2
が分かります。
底の変換公式は,底の「a→c」という変換です。
c
がなんでも良いというのが面白いです。
Tag:数学2の教科書に載っている公式の解説一覧