三乗根（立方根）の意味と計算をわかりやすく

任意の実数 $a$ に対して，三乗して $a$ になる実数が1つ存在します。これを $\sqrt[3]{a}$ と書きます。

$a$ がマイナスでも三乗根はただ1つ存在します。

※2乗してマイナスになる実数は存在しないので $\sqrt{負の数}$ は実数の範囲で存在しませんでしたが，$\sqrt[3]{負の数}$ は存在します。

三乗根の近似値の求め方

例えば，2の3乗根は $\sqrt[3]{2}\fallingdotseq 1.2599$ です。この近似値の求め方を3通り紹介します。

• とにかく近似値が知りたい場合：
  Google 検索で「cubic root of 2」と検索しましょう。

• 大雑把な値を手計算したい場合：
  有効数字2ケタ程度なら，愚直に計算することもできます。例えば $1.2^3=1.728$，$1.3^3=2.197$ なので $1.2<\sqrt[3]{2}<1.3$ です。

• 数値計算したい場合（難しい）：
  $f(x)=x^3-2$ という関数にニュートン法を使えばよいです。→ニュートン法の解説とそれを背景とする入試問題

三乗根を含む式の計算

• $\sqrt[3]{a^3}=a$ です。ルートの場合は $\sqrt{a^2}=|a|$ でしたが，三乗根の場合はそのまま外せます。

• $\sqrt[3]{a}\sqrt[3]{b}=\sqrt[3]{ab}$ です。例えば，$\sqrt[3]{2}\sqrt[3]{4}=\sqrt[3]{8}=2$ のように計算できます。

• $\dfrac{\sqrt[3]{a}}{\sqrt[3]{b}}=\sqrt[3]{\dfrac{b}{a}}$ です。例えば，$\dfrac{\sqrt[3]{16}}{\sqrt[3]{2}}=\sqrt[3]{\dfrac{16}{2}}=\sqrt[3]{8}=2$ のように計算できます。

• $\sqrt[3]{a^3b}=a\sqrt[3]{b}$ です。一部を三乗根の外側に出せます。例えば，$\sqrt[3]{24}=2\sqrt[3]{3}$ です。

ここから複素数の三乗根を考えますが，それに向けて重要な役割を果たすのが「1の三乗根」です。

1の三乗根のうち複素数のもの $\dfrac{-1\pm\sqrt{3}i}{2}$ （のうちのどちらか1つ）を $\omega$（オメガ）と表します。１の三乗根オメガを用いた計算と因数分解

以下，$\omega=\dfrac{-1+\sqrt{3}i}{2}$ とします。1の3乗根です。

例えば，$8i$ の3乗根は $-2i,i\pm\sqrt{3}$ の 3つです。複素数平面で表すと，図のように正三角形をなします。

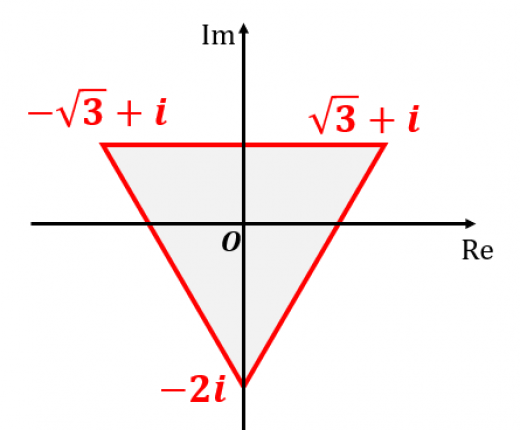
なお，三乗根が理解できれば，四乗根や一般の $n$ 乗根も同じように理解できます。→累乗根の定義と具体例