その他
更新
その他 に関する30記事をまとめました。くわしくは各リンク先を見てください。
不等号の意味と読み方,および3種類の等号つき不等号について整理しました。
-
: 指数関数 のこと
-
: 自然対数 のこと
-
: 10を底とする対数 のこと(を表す場合が多い)
還元率 は,割引率 に相当する。
当サイトの管理人が, ルール(定義)と事実(定理)をきちんと区別してほしい! というテーマで、算数の本を出版しました。
は, のことを表す。
IMO以外にもたくさんの数学コンテストが世界中で開催されています。
各地の数学コンテストの概要と過去問の場所を紹介します。
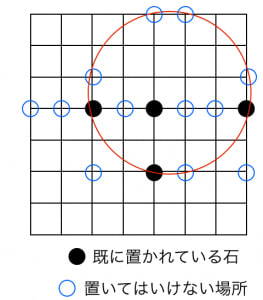
共円は,格子点上に同一円周上に四点以上石があるような状態(共円)を作らないように石を置いていくゲームです。
閏年(うるう年)は400年に97回来るような規則になっている。
「 パーセントの坂」とは「100メートル横移動したときに メートル上がるくらいの角度の坂」のこと
対数グラフとは,対数目盛を使ったグラフのことです。普通の目盛では「0から1」「1から2」が同じ1目盛分になりますが,対数目盛では,「1から10」「10から100」が同じ1目盛分になります。
超越数とは,代数方程式の解ではない数のこと。

移動時間短縮のために新しい道路を作った結果,移動時間がかえって長くなってしまうことがある。
音階と周波数比についての話題を紹介します。等比数列,累乗根という数学の基本的な道具が登場します。
マルバツゲーム(三目並べ)では両者が頑張れば必ず引き分けになる。
オーダー記法(ランダウの記号)は,無限大でのふるまいや 付近でのふるまいを大雑把に評価するのに用いられる。
はそれぞれ のいずれかとする。このとき,
となる をレビチビタ記号(エディントンのイプシロン)という。
LP:線形計画問題
QP:二次計画問題
QCQP:二次制約つき二次計画問題
SOCP:二次錐計画問題
SDP:半正定値計画問題
大学ではどのような数学を学ぶのか,高校数学と関連させつつ整理しました。より抽象的で美しい世界が待っています。
は黄金比と呼ばれ,いろいろな場所に出現する。
→黄金比が現れるいろいろな例(方程式・図形・数列)と現れる理由
問題の集合(クラス)PとNPが等しくないという予想です。
- 「P」というのは,多項式時間で解ける問題のクラス,つまり「パソコンで解きやすい」問題です。
- 「NP」というのは,多項式時間で正解が本当に正しいか判定できる問題のクラスです。
受験勉強の息抜きにテトリスをどうぞ。ぜひ一度hatetrisをやってみてください,感動します!
日本数学オリンピックの予選・本選,国際数学オリンピックの合格基準を整理しました。
-
アクチュアリーの資格を取る
-
アクチュアリーを採用している企業から内定をもらう
数学や物理では などのギリシャ文字に関して,ある程度決まった使い方があります。
ミレニアム懸賞問題の概要,一覧,そしてそのうちのいくつかについての大雑把な説明をします。
Wolfram Alphaという無料のサービスがいろいろな計算に使えて素晴らしいので紹介します。高校数学レベルの計算でも重宝します。
なる直角三角形 について
高校数学の美しい物語が本になりました!
新版(2024年発売)と旧版(2016年発売)があります。新版の方が内容が少しだけ多いです。





