複素関数論(複素解析)まとめ
更新
複素関数論(複素解析)は,複素数上で定義された関数の微積分などを扱う分野です。
- 複素関数の微積分の基本
- 美しい複素積分の理論(コーシーの積分定理・ローラン展開・留数定理)
- 楽しい応用(実積分の計算・代数学の基本定理の証明・三角関数の等式証明)
などを,勉強しやすい順番で紹介していきます。より詳しい説明は各リンク先を参照してください。
複素数の指数関数・対数関数
複素数の指数関数・対数関数
複素関数の例として,高校数学で習う指数関数・対数関数の定義域を複素数に広げたものが挙げられます。
複素数 に対して,指数関数 は以下の式で定義される:
特に, が成立する(オイラーの公式)。
詳細は →オイラーの公式と複素指数関数
でない複素数
に対してその対数は,
これは多価関数になる。また,対数関数をもとに複素数ベキも定義できる。すると, の主値は になる。
複素関数の微積分の定義
複素関数の微積分の定義
複素関数の微分を考えます。
複素関数 が で微分可能とは,
が存在するという意味。
ただし, が へどのように近づいても同じ極限値が存在しないといけないという意味で,実関数の場合よりも厳しい条件です。条件が厳しいため,複素関数では1階微分可能なら無限回微分可能というすさまじい定理が成立します。微分可能な関数を正則関数と言います。
複素関数 の積分は,区分的になめらかな曲線 上での線積分 として定義される。
複素関数の積分を理解するには「線積分」の知識が必要です。実1変数関数と異なり入力が2次元平面(複素数平面)上に広がっており,積分値は経路に依存するためです。
複素関数の積分の性質
複素関数の積分の性質
複素関数の積分には,おもしろい性質がたくさんあります。
正則関数をぐるっと一周積分すると値は になる。つまり,
を単連結な(つながっていて穴がない)領域 内で正則な複素関数とする。 は 内の単純閉曲線(自分自身と交わらない閉じた曲線)とするとき
(単純)閉曲線 と, で囲まれた領域 を考える。 上で 級の任意の関数 , に対して以下が成り立つ。
これは複素積分に関する定理というよりは,コーシーの積分定理の証明に現れる定理です。
詳細は →グリーンの定理
正則関数の値は,自分を囲む曲線上での積分値で表せる。つまり,以下が成立する。
- を単純閉曲線(自分と交わらない閉じた曲線)で囲まれた領域とする。
- を領域 で正則な関数とする。
このとき の内部の任意の点 で となる(線積分の向きは反時計回り,より厳密には領域の内側から見て左周りに定める)。
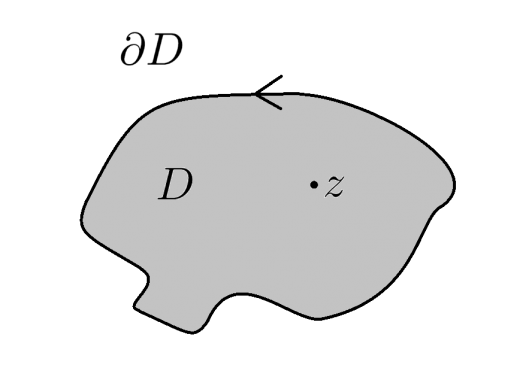
コーシーの積分定理は(コーシーの積分公式から導かれますが),コーシーの積分公式とは別物です。
詳細は →コーシーの積分公式とその応用~グルサの定理・モレラの定理
正則関数は微分可能な点のまわりでテイラー展開できるが,微分可能でない点(孤立特異点)のまわりでも,テイラー展開をマイナス乗まで拡張したような展開(ローラン展開)ができる。つまり,
で正則(微分可能)な複素関数 は,以下のようにべき級数展開できる。 ただし,各係数 は で計算できる ( は を満たす実数ならなんでもよい)。
留数定理
留数定理
5~8まで理解すれば,楽しい応用が待っています。まずは,積分計算に使える留数定理です。
大きい周回積分=内部の各孤立特異点まわりでの積分の和
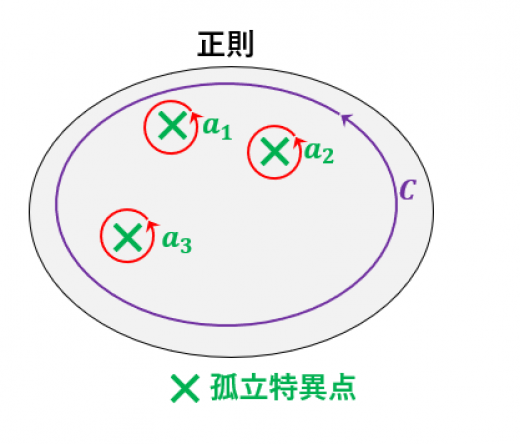
正確には以下の通り:
- 単連結な領域 内に,区分的になめらかな単純閉曲線 がある
- は で囲まれた領域で有限個の点 を除いて正則
このとき, である。ただし, は の での留数とする。
証明には5.コーシーの積分定理を使い,留数の計算には8.ローラン展開を使います。
詳細は →留数定理
留数定理を使うことで,実解析の範囲では計算が困難であった定積分が計算できる場合がある。例えば,
計算の詳細は,それぞれ以下の記事で解説しています。
応用:方程式の解の個数
応用:方程式の解の個数
5~8の楽しい応用は,留数定理だけではありません。
有界な整関数は定数関数のみである。ただし,複素平面 全体で正則な関数を整関数という。
リュウビルの定理を使うことで代数学の基本定理(複素数係数の 次方程式は複素数の範囲で重複度も含めて 個の解を持つ)が証明できます。
特殊な複素積分によって複素関数の零点・極の個数が計算できる。正確には以下の通り。
をなめらかな曲線に囲まれた有界な領域とする。
を 上で極も零点も持たない 上の有理型関数とする。
の 上の零点の(重複度を含めた)個数を ,極の(重複度を含めた)個数を とする。このとき である。

応用:部分分数分解,因数分解
応用:部分分数分解,因数分解
「11.リュウビルの定理」を使って三角関数の等式が証明できるのもおもしろいです。
詳細は →三角関数の部分分数分解
さらに,13をもとに以下の14が導けます。
その他の話題
その他の話題
リーマン球面とは,複素平面 に無限遠点 を追加したものである。
詳細は →リーマン球面と無限遠点
を領域 上の正則関数とする。
- が 内のある線分・なめらかな曲線上( など)で一致するとき, 全体でも一致する。
- が 内の開集合 上で一致するとき, 全体でも一致する。
という複素関数の等式を証明したいとき,一致の定理を用いれば,ほんの一部での一致を確認すればOKと言えます。「8. ローラン展開」を使って証明できます。
詳細は →一致の定理
正則かつ有界なら特異点は除去可能。正確には,以下の通り。
は, を孤立特異点として持ち, 上で正則かつ有界な関数とする。このとき, は除去可能特異点である。すなわち, を適切に追加で定めれば は 上で正則にできる。
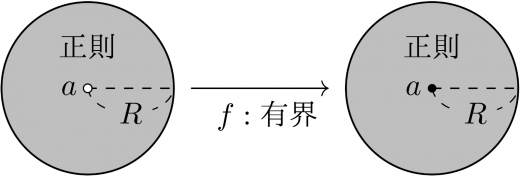
例えば,留数計算に使う定理を証明する際に役立ちます。
詳細は →リーマンの可除特異点定理
有界な領域 上の正則関数 について,ある で が最大値を取るとき, は定数関数である。
詳細は →最大値の原理とシュワルツの補題
ローラン展開,リュウビルの定理,リーマンの可除特異点定理など,名前がかっこいいものが多いです。





