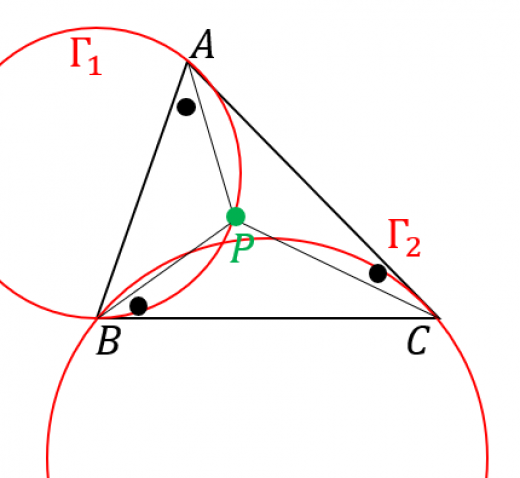
ブロカール点の定義に現れる角度の大きさ ω \omega ω ∠ P A B = ∠ P B C = ∠ P C A = ω \angle PAB=\angle PBC=\angle PCA=\omega ∠ P A B = ∠ PBC = ∠ PC A = ω
ブロカール角の性質1
1 tan ω = 1 tan A + 1 tan B + 1 tan C \dfrac{1}{\tan\omega}=\dfrac{1}{\tan A}+\dfrac{1}{\tan B}+\dfrac{1}{\tan C} tan ω 1 = tan A 1 + tan B 1 + tan C 1
※例えば A = 9 0 ∘ A=90^{\circ} A = 9 0 ∘ 1 tan A = 0 \dfrac{1}{\tan A}=0 tan A 1 = 0
証明
1 tan A = b 2 + c 2 − a 2 4 S ⋯ ( ∗ ) \dfrac{1}{\tan A}=\dfrac{b^2+c^2-a^2}{4S}\cdots(*) tan A 1 = 4 S b 2 + c 2 − a 2 ⋯ ( ∗ )
1の右辺は ( ∗ ) (*) ( ∗ ) a 2 + b 2 + c 2 4 S \dfrac{a^2+b^2+c^2}{4S} 4 S a 2 + b 2 + c 2 タンジェントの美しい関係式 の(iii)にもあるように比較的有名。
1の左辺は,3つの小さい三角形にそれぞれ ( ∗ ) (*) ( ∗ ) 4 S P A B tan ω = P A 2 + c 2 − P B 2 4 S P B C tan ω = P B 2 + a 2 − P C 2 4 S P C A tan ω = P C 2 + b 2 − P A 2 \dfrac{4S_{PAB}}{\tan\omega}=PA^2+c^2-PB^2\\
\dfrac{4S_{PBC}}{\tan\omega}=PB^2+a^2-PC^2\\
\dfrac{4S_{PCA}}{\tan\omega}=PC^2+b^2-PA^2 tan ω 4 S P A B = P A 2 + c 2 − P B 2 tan ω 4 S PBC = P B 2 + a 2 − P C 2 tan ω 4 S PC A = P C 2 + b 2 − P A 2 4 S tan ω = a 2 + b 2 + c 2 \dfrac{4S}{\tan\omega}=a^2+b^2+c^2 tan ω 4 S = a 2 + b 2 + c 2 4 S 4S 4 S a 2 + b 2 + c 2 4 S \dfrac{a^2+b^2+c^2}{4S} 4 S a 2 + b 2 + c 2
1の結果を使って,以下を証明できます。
ブロカール角の性質2
ω ≦ 3 0 ∘ \omega\leqq 30^{\circ} ω ≦ 3 0 ∘
証明を2通り紹介します。
証明(方法1)
1の証明の途中式より
1 tan 2 ω = ( a 2 + b 2 + c 2 ) 2 16 S 2 \dfrac{1}{\tan^2\omega}=\dfrac{(a^2+b^2+c^2)^2}{16S^2} tan 2 ω 1 = 16 S 2 ( a 2 + b 2 + c 2 ) 2 ヘロンの公式 の「辺の長さが無理数の場合」版より
1 tan 2 ω = ( a 2 + b 2 + c 2 ) 2 2 ( a 2 b 2 + b 2 c 2 + c 2 a 2 ) − ( a 4 + b 4 + c 4 ) \dfrac{1}{\tan^2\omega}=\dfrac{(a^2+b^2+c^2)^2}{2(a^2b^2+b^2c^2+c^2a^2)-(a^4+b^4+c^4)} tan 2 ω 1 = 2 ( a 2 b 2 + b 2 c 2 + c 2 a 2 ) − ( a 4 + b 4 + c 4 ) ( a 2 + b 2 + c 2 ) 2
次に,a 4 + b 4 + c 4 = x , a 2 b 2 + b 2 c 2 + c 2 a 2 = y a^4+b^4+c^4=x,a^2b^2+b^2c^2+c^2a^2=y a 4 + b 4 + c 4 = x , a 2 b 2 + b 2 c 2 + c 2 a 2 = y
1 tan 2 ω = x + 2 y 2 y − x \dfrac{1}{\tan^2\omega}=\dfrac{x+2y}{2y-x} tan 2 ω 1 = 2 y − x x + 2 y
目標は,ω ≦ 3 0 ∘ \omega\leqq 30^{\circ} ω ≦ 3 0 ∘ tan ω < 9 0 ∘ \tan\omega< 90^{\circ} tan ω < 9 0 ∘ 1 tan 2 ω ≧ 3 \dfrac{1}{\tan^2\omega}\geqq 3 tan 2 ω 1 ≧ 3 x + 2 y ≧ 3 ( 2 y − x ) x+2y\geqq 3(2y-x) x + 2 y ≧ 3 ( 2 y − x ) x ≧ y x\geqq y x ≧ y 有名不等式a^2+b^2+c^2≧ab+bc+ca より成立。
※方法1の後半の議論は三角形における距離の二乗の和の公式 の応用問題と非常に似ていておもしろいです。
証明(方法2)
鋭角三角形の場合で証明する。
f ( x ) = 1 tan x f(x)=\dfrac{1}{\tan x} f ( x ) = tan x 1
f ′ ′ ( x ) = 2 tan x sin 2 x f''(x)=\dfrac{2}{\tan x\sin^2 x} f ′′ ( x ) = tan x sin 2 x 2
より,0 < x < π 2 0< x< \dfrac{\pi}{2} 0 < x < 2 π イェンゼンの不等式 より,
f ( A ) + f ( B ) + f ( C ) ≧ 3 f ( A + B + C 3 ) f(A)+f(B)+f(C)\geqq 3f\left(\dfrac{A+B+C}{3}\right) f ( A ) + f ( B ) + f ( C ) ≧ 3 f ( 3 A + B + C )
つまり,
1 tan A + 1 tan B + 1 tan C ≧ 3 3 \dfrac{1}{\tan A}+\dfrac{1}{\tan B}+\dfrac{1}{\tan C}\geqq \dfrac{3}{\sqrt{3}} tan A 1 + tan B 1 + tan C 1 ≧ 3 3
これと 1 1 1 tan ω ≦ 1 3 \tan\omega\leqq\dfrac{1}{\sqrt{3}} tan ω ≦ 3 1
つまり ω ≦ 3 0 ∘ \omega\leqq 30^{\circ} ω ≦ 3 0 ∘