体積を求める公式一覧
体積を計算するための公式を整理しました。立方体からはじめて難しい公式まで一覧にしましたが,特に重要なのは,
- 柱体の体積:底面積×高さ
- 錐体の体積:底面積×高さ÷3
の2種類です。
立方体・直方体の体積
立方体・直方体の体積
立方体の体積
体積=「1辺の長さ」の3乗
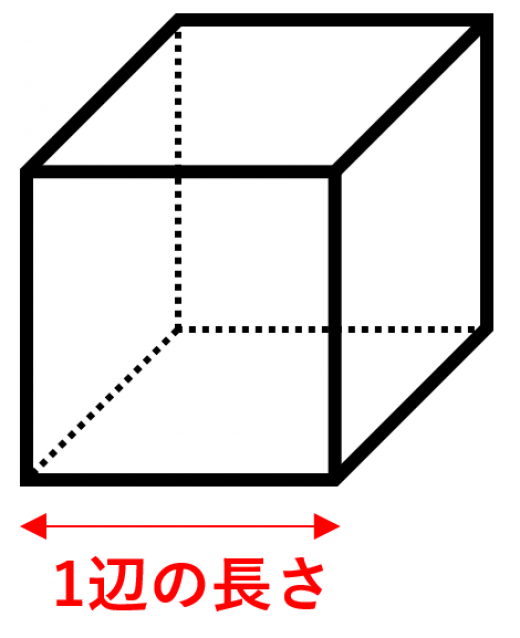
例えば,1辺の長さが2の立方体の体積は, です。
直方体の体積
- 体積=縦×横×高さ
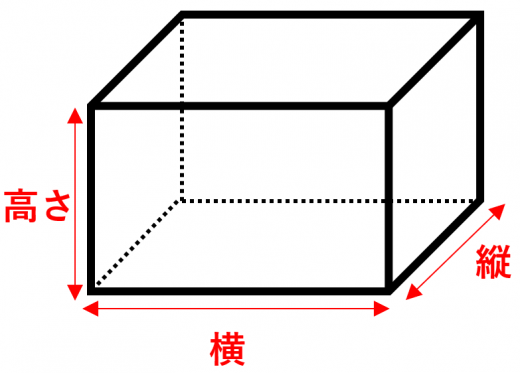
例えば,縦=2,横=5,高さ=3である直方体の体積は, です。
柱体の体積
柱体の体積
すべて 体積=底面積×高さ です。
円柱の体積
- 体積=底面積×高さ
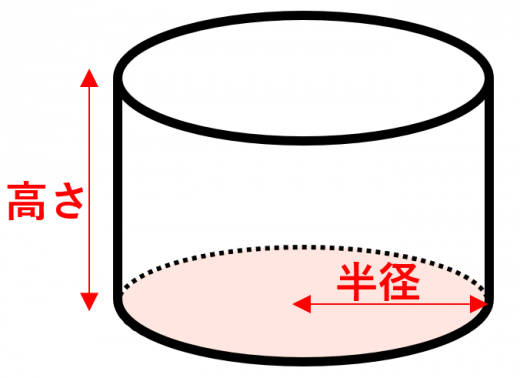
さらに,底面積は「半径×半径×円周率」なので,
- 体積=半径×半径×円周率×高さ
と表すこともできます。例えば,半径=2,高さ=3である円柱の体積は, です。ただし, は円周率です。
三角柱の体積
- 体積=底面積×高さ
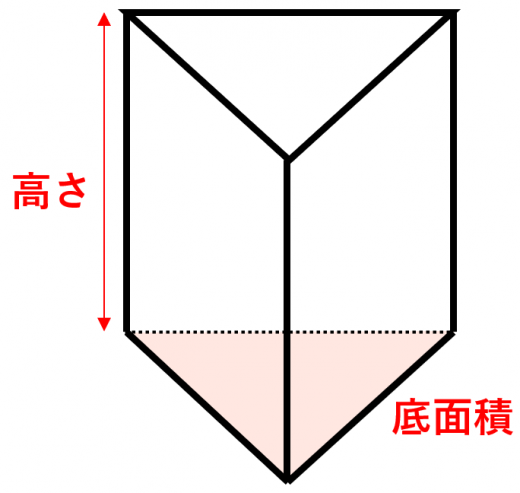
例えば,底面積=4,高さ=3である三角柱の体積は, です。
さらに,底面積は「底辺×高さ÷2」なので,
- 体積=底面の底辺の長さ×底面の高さ÷2×高さ
と表すこともできます。
四角柱の体積
- 体積=底面積×高さ

例えば,底面積=4,高さ=3である四角柱の体積は, です。
ちなみに,直方体・立方体も四角柱の一種です。
錐体の体積
錐体の体積
すべて 体積=底面積×高さ÷3 です。
円錐の体積
- 体積=底面積×高さ÷3
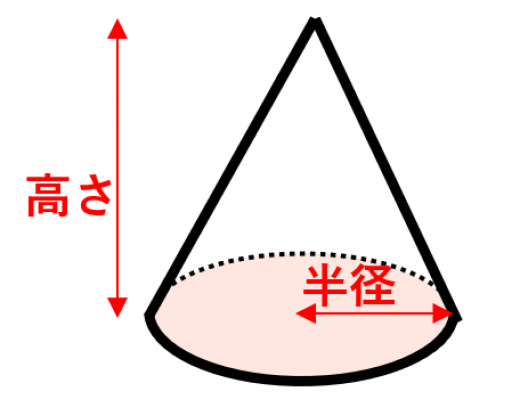
さらに,底面積は「半径×半径×円周率」なので,
- 体積=半径×半径×円周率×高さ÷3
と表すこともできます。例えば,半径=2,高さ=3である円錐の体積は, です。ただし, は円周率です。
三角錐の体積
- 体積=底面積×高さ÷3
 です。例えば,底面積=4,高さ=3である三角錐の体積は, です。
です。例えば,底面積=4,高さ=3である三角錐の体積は, です。
さらに,底面積は「底辺×高さ÷2」なので,
- 体積=底面の底辺の長さ×底面の高さ÷2×高さ÷3
と表すこともできます。
四角錐の体積
- 体積=底面積×高さ÷3

例えば,底面積=4,高さ=3である四角錐の体積は, です。
ちなみに,錐体の体積で÷3をする理由は少しむずかしいです。錐体の体積に1/3がつくことの2通りの説明で解説しています。
球・正四面体の体積
球・正四面体の体積
球や正四面体の体積は,高校入試・大学入試でも活躍します。
球の体積
- 体積=
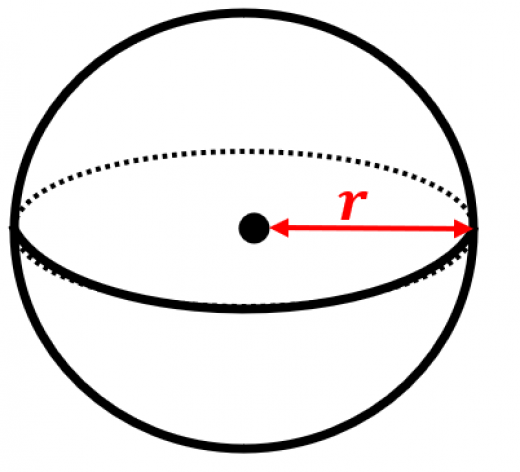 は円周率, は球の半径です。
は円周率, は球の半径です。
正四面体の体積
- 体積=
 は正四面体の1辺の長さです。
は正四面体の1辺の長さです。
マニアックな立体の体積
マニアックな立体の体積
以下は覚える必要はありません。
-
1辺の長さが である正二十面体の体積は,
体積=
→正二十面体の対角線・体積・内接球などを座標で計算 -
ドーナツの体積は,
体積=
→ドーナツ(トーラス体・円環体)の体積・表面積を2通りの方法で計算 -
楕円体: の体積は,
体積=
→楕円体・回転楕円体の意味と体積・表面積
たくさん公式がありますが,覚えるべき公式は少ないです。











