検算テクニック に関する19記事をまとめました。くわしくは各リンク先を見てください。
(i)1辺の長さが
a
の正三角形の面積
S
は,
S=43a2
(ii)1辺の長さが
a
の正四面体の体積
V
は,V=122a3
→正三角形の面積,正四面体の体積を求める公式
三角関数の 00 不定形の極限を求める問題は,マクローリン展開を用いた多項式近似で素早く解くことができる。
→三角関数の不定形極限を機械的な計算で求める方法
覚えておくと便利な常用対数
- log102≒0.3010
- log103≒0.4771
- log107≒0.8451
- logex≒2.3log10x
→常用対数の覚え方と検算への応用
∫eaxcosbx dx=a2+b2eax(acosbx+bsinbx)+C
∫eaxsinbx dx=a2+b2eax(asinbx−bcosbx)+C
→三角関数と指数関数の積の積分を一発で求める公式
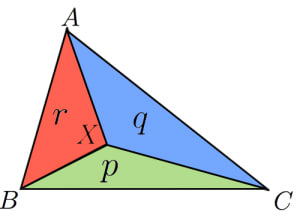
三角形
ABC
内に点
X
があり,pXA+qXB+rXC=0
が成立するとき,面積比は
△XAB:△XBC:△XCA=r:p:q
→ベクトルの定番問題を一瞬で解く公式
xy 座標平面における直線の方程式には,いくつかの表し方がある。
- y=mx+n(傾きと切片による表現)
- ax+by+c=0(一般形)
→直線の方程式の一般形が嬉しい3つの理由
検算は,数学の試験で高得点を取るためにとても重要です!
→検算の重要性と具体的なテクニック5つ
三次関数のグラフの対称性

三次関数のグラフに関して以下の性質が成り立つ:
-
変曲点に関して点対称である
-
図において,A,B,C,D,E
は等間隔に並んでいる(4等分の法則)
(C
は変曲点,B,D
は極大,極小点,A,E
は極大,極小点と同じ高さの点の
x
軸への射影)
→三次関数の対称性と4等分の法則
テクニック1
y=g(x)f(x)
が
x=α
で極値を取るとき,g′(α)=0
ならその値は
g′(α)f′(α)
である。
→分数関数の極値を求める2つのテクニック
ロピタルの定理の概要
x→alimg(x)f(x)
が
00
または
∞∞
の不定形で「ある条件」を満たせば,
x→alimg(x)f(x)=x→alimg′(x)f′(x)
→ロピタルの定理の条件と例題
1/3公式
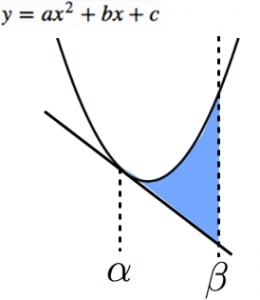
- 放物線 y=ax2+bx+c
- 放物線と x=α で接する接線
- x=β
という3つのグラフで囲まれた部分の面積は,
3∣a∣∣β−α∣3
→1/3公式と1/12公式の意味と証明【二次関数・三次関数と面積】
トレミーの定理
円に内接する四角形
ABCD
において,
AB×CD+AD×BC=AC×BD
が成立する。これをトレミーの定理と言う。

→トレミーの定理とその3通りの証明,応用例
攪乱順列(完全順列)の個数
n≧2 とする。1 から n までの整数を並び替えてできる順列のうち,すべての i について「i 番目が i でない」を満たすものの個数 an は
an=n!k=2∑nk!(−1)k
→攪乱順列(完全順列)の個数を求める公式
同じものを含む円順列の個数はバーンサイドの公式を使って求めることができる:
円順列の個数=∣G∣1g∈G∑ϕ(g)
→同じものを含む円順列の裏技公式
三項間漸化式の特性方程式の解を
α,β
とおくと,漸化式の一般項は
an=Aαn+Bβn
と表される。A,B
は初期条件から求める。
→三項間漸化式の3通りの解き方
ラグランジュの三角恒等式(Lagrange's trigonometric identities)
(位相が等差数列なら)三角関数の和を計算できる:
k=0∑nsin(θ+kϕ)=sin2ϕsin(2(n+1)ϕ)sin(θ+2nϕ)k=0∑ncos(θ+kϕ)=sin2ϕsin(2(n+1)ϕ)cos(θ+2nϕ)
→位相が等差数列である三角関数の和の公式
シンプソンの公式
f(x)
が3次以下の関数のとき,
∫abf(x)dx=6(b−a){f(a)+4f(2a+b)+f(b)}
→シンプソンの公式の証明と例題
O(0,0,0),A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3) を頂点とする四面体の体積は 61∣detM∣ となる。
→四面体の体積を求める2つの公式with行列式
対称式の展開した式に,ka2 という項があれば kb2,kc2 という項もあります。 ka2b という項があれば kab2,kb2c,kbc2,kc2a,kca2 もあります。
→対称式を素早く正確に展開する3つのコツ









