直辺四面体(垂心四面体)と24点球の定理
四面体において以下の5つの条件は同値です。このいずれか(したがって全て)を満たす四面体のことを直辺四面体(直稜四面体,垂心四面体)と言います。
四面体 において,以下は同値:
-
,
-
,,
-
四面体 に垂心が存在する(頂点から対面におろした4本の垂線が1点で交わる)。
-
-
対辺の中点同士を結ぶ3本の線分の長さが等しい
1つずつ説明していきます。
なお,後半の24点球の定理は難しいですが,それ以外は大学入試レベルです。
直辺四面体
直辺四面体
四面体において,「頂点を共有しない2つの辺」のことを対辺と呼ぶことにします。
3組の対辺がそれぞれ直交する四面体のことを直辺四面体と言います。多面体における辺のことを稜と言うので,直辺四面体のことを直稜四面体とも言います。
まずは,冒頭の条件1と2が同値であることを示します。つまり,2組の対辺がそれぞれ直交すれば残りの1組も直交することを示します。
各点の位置ベクトルを とおきます。ベクトルで計算していくだけです。
ならば,
つまり
同様に, ならば
この2式の右辺は等しいので左辺も等しい:
よって
つまり,直辺四面体は
という3つの値がすべて等しい四面体とも言えます。
垂心四面体
垂心四面体
三角形において,頂点から対辺に下ろした3本の垂線は1点で交わります。この点を三角形の垂心と言います。→垂心の存在の3通りの証明
四面体についても垂心を考えてみます。各頂点から対面へ下ろした4本の垂線が1点で交わるとき,この点を四面体の垂心と言います。一般の四面体には垂心が存在するとは限りませんが,直辺四面体には垂心が存在します。そのため,直辺四面体は垂心四面体と呼ばれることもあります。
では条件2(対辺直交)と条件3(垂心の存在)が同値であることを証明してみます。
こちらは計算するだけなので簡単。垂心 があれば,
より
より
以上2式より
つまり
次が一番むずかしいです。外心をベクトルの始点にするとうまくいきます。
天下り的だが,
とおく。ただし,各ベクトルの始点を四面体の外心 とする。
(最後の等号は であることから)
よって なら
同様に もわかり, は と直交する。残りの3本 も対称性より同様。
四面体のモンジュ点
四面体の垂心に関する余談です。
- 任意の四面体 において「ある辺の中点を通りその対辺と垂直な平面」は6枚あるが,すべて1点を通る。この点をモンジュ点と呼ぶ。
- モンジュ点の位置ベクトルは である。
- 特に垂心四面体ならモンジュ点は垂心と一致する。
1と2の証明は簡単です。計算してみてください。3は上記の「対辺直交なら垂心があることの証明」で見たように位置ベクトルの表記が両者で一致することからわかります。
直辺四面体の他の性質
直辺四面体の他の性質
次は条件4です。さきほどの紫字の条件と条件4: が同値であることを示します。ベクトルで計算するだけなので簡単です。
とおくと,
より条件4とさきほどの紫字の条件は同値。
次は条件5です。同じくさきほどの紫字の条件と条件5が同値であることを示します。計算するだけです。
と の中点を とおくと,
ただし,
とおいた。対辺の中点同士を結ぶ3本の線分の長さが等しい
オイラー線と24点球の定理
オイラー線と24点球の定理
九点円の定理の三次元バージョンです。九点円については九点円の定理の証明と諸性質を参照してください。
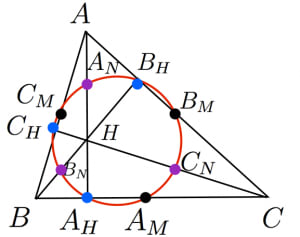
直辺四面体において,各面の「九点円の定理」に登場する9点は合計24点あり,それらは同一球面上にある。
面が つなので 点ありそうですが,9点のうち「各辺の中点3つ」と「垂線の足3つ」は2つの面で重複しているので,重複分 を除いて 点です。
直辺四面体 の外心を ,垂心を , の中点を とおく。三角形 の外心を ,垂心を ,九点円 の中心を とおく。 なども同様に定める。
が と直交すること(★)を示せば良い。
-
もし(★)が示せれば:
を中心とし を通る球面 を考える。 (★)と同様に は と直交するので は も通る( も も の中点を通ることに注意)。同様に は も通る。 -
(★)は以下のようにわかる:
まず定義より は同一直線上にあり,三角形 のオイラー線から も別の同一直線上にある。この2本の直線は同一平面上にある(なぜなら と が平行だから)。一方, は の中点で は の中点。以上より は と平行。

特殊な四面体
特殊な四面体
-
直辺四面体は特殊な四面体です。
-
似たような概念として等面四面体もあります。対辺の長さがそれぞれ等しい四面体です。→等面四面体とその性質
-
直辺四面体かつ等面四面体なら正四面体です。証明してみてください。
-
あまり似ていないですが,三直角四面体(直角三角錐)も特殊な四面体です。→四平方の定理(図形の面積と正射影)
直辺四面体は「ベクトルで計算」,等面四面体は「直方体に埋め込み」です。











